|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ПЛЮККЕРОВЫ КООРДИНАТЫЗначение ПЛЮККЕРОВЫ КООРДИНАТЫ в математической энциклопедии: координаты прямой в трехмерном пространстве, шесть чисел р 01, p02, p03, p04, p05, p06 из к-рых первые три являются координатами направляющего вектора lпрямой L, а вторые три - моменты этого вектора относительно начала координат. Пусть прямая Lпроходит через точки X и Y с проективными координатами ( х 0, x1, . .., x3).и (y0, y1, . . ., y3).соответственно П. к. этой прямой являются числа П. к. применяют в линейчатой геометрии. Впервые были рассмотрены Ю. Плюккером (J. Plucker, 1869). Иногда вместо П. к. используют Клейна координаты ( х 0, . . ., х 5), связанные с П. к. формулами: Естественно рассматривать П. к. как координаты в р-мерном векторном подпространстве n-мерного векторного пространства V. При этом они понимаются как совокупность чисел, равных П. к. симметричны по всем индексам. Число существенных П. к. равно При замене базиса Wи фиксированном базисе VП. к. умножаются на одно и то же ненулевое число. При замене базиса Vи фиксированном базисе WП. к. преобразуются как координаты контравариантного тензора валентности р (см. Поливектор). Два подпространства совпадают тогда и только тогда, когда их П. к., вычисленные в одном и том же базисе пространства V, отличаются лишь ненулевым множителем. Принадлежность вектора хподпространству Wзаписывается в виде линейных уравнений с коэффициентами, являющимися П. к. подпространства W. В этих уравнениях i1<i2<. . .<ip- всевозможные наборы из чисел 1, 2, . . ., п. Л. П. Купцов. |
|
|
|

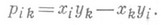

 - субдетерминантам
- субдетерминантам 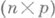 -матрицы ( а 1, а 2, . . ., а р), столбцы а i,
-матрицы ( а 1, а 2, . . ., а р), столбцы а i,  , к-рой являются столбцами координат (в каком-либо базисе пространства V).базисных векторов подпространства W. Если
, к-рой являются столбцами координат (в каком-либо базисе пространства V).базисных векторов подпространства W. Если  - компоненты столбца
- компоненты столбца  то П. к. (или грассмановы координаты) являются числа
то П. к. (или грассмановы координаты) являются числа 
 .
.