|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ПЛОТНОСТЬ ПОСЛЕДОВАТЕЛЬНОСТИЗначение ПЛОТНОСТЬ ПОСЛЕДОВАТЕЛЬНОСТИ в математической энциклопедии: понятие общей аддитивной теории чисел, изучающей законы сложения последовательностей общего вида. П. п. является мерой того, какая часть из последовательности всех натуральных чисел принадлежит данной последовательности где
Плотность d(A)=l тогда и только тогда, когда Асовпадает с множеством N0 всех целых неотрицательных чисел. Пусть А+В - арифметич, сумма последовательностей А={ а k} и В= {bi}, т. е. множество А+В={ak+bi}, где числа ak+bi берутся без повторений. При А=В полагают 2А - А-{-А, аналогично ЗА=А+А+А и т. д. Если hA=N0, то Аназ. базисом h- гопорядка. При исследовании структуры множеств, получающихся в результате суммирования последовательностей, заданных лишь их плотностями, используются теоремы о плотности суммы двух последовательностей: Из неравенства Шнирельмана следует, что всякая последовательность положительной плотности есть базис конечного порядка. Применение этого факта к аддитивным задачам, в к-рых часто суммируются последовательности нулевой плотности, осуществляется посредством предварительного конструирования из заданных последовательностей новых с положительной плотностью. Напр., с помощью методов решета доказывается, что последовательность {р}+{p}, где рпробегает простые числа, обладает положительной плотностью. Отсюда следует теорема Шнирельмана: существует такое целое число с 0>0) что любое натуральное число есть сумма не более с 0 простых чисел. Эта теорема дает решение т. н. ослабленной проблемы Гольдбаха (см. также Аддитивная теория чисел). Разновидностью понятия П. п. является понятие асимптотический плотности, частным случаем к-рой будет натуральная плотность. Понятие П. п. обобщается на числовые последовательности, отличные от натурального ряда, напр. на последовательности целых чисел в полях алгебраич. чисел. В результате удается изучать базисы в алгебраич. полях. Лит.:[1] Гельфонд А. О., Линник Ю. В., Элементарные методы в аналитической теории чисел, М., 1962; [2] Оstmann H.-H., Additive Zahlentheorie, Bd 1-2, В., 1956. Б. М. Бредихин. |
|
|
|

 целых чисел a0=0<1
целых чисел a0=0<1 а 1< а 2<...<
а 1< а 2<...< . Под понятием П. п. имеется в виду плотность d(A).(введенная в 1930 Л. Г. Шнирельманом) последовательности А, а именно:
. Под понятием П. п. имеется в виду плотность d(A).(введенная в 1930 Л. Г. Шнирельманом) последовательности А, а именно:

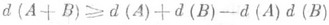 - неравенство Шнирельмана,
- неравенство Шнирельмана, - неравенство Манна - Дайсона.
- неравенство Манна - Дайсона.