|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
АБЕЛЕВА ГРУППАЗначение АБЕЛЕВА ГРУППА в математической энциклопедии: разрешимости алгебраич. уравнений в радикалах. Обычно для обозначения операции в А. г. используется аддитивная запись, т. е. знак + для самой операции, наз. сложением, знак 0 для нейтрального элемента, наз. нулем (в мультипликативной записи он наз. единицей). Примеры А. г. Все циклические группы - абе-левы, в частности аддитивная группа целых чисел - абелева. А. г. будут всевозможные прямые суммы циклич. групп, аддитивная группа рациональных чисел Q(являющаяся локально циклической группой, т. е. группой, все конечно порожденные подгруппы к-рой циклические), группы типа Свободное объединение в многообразии А. г. совпадает с прямой суммой. Свободная абелева группа есть прямая сумма нек-рого множества бесконечных циклич. групп. Всякая подгруппа свободной А. г.- свободная А. г. Совокупность всех элементов конечного порядка А. г. образует подгруппу, наз. периодической частью А. г. Факторгруппа А. г. по ее периодич. части является группой без кручения. Таким образом, всякая А. г.- расширение периодич. А. г. при помощи А. г. без кручения. Это расширение не всегда расщепляемо, т. е. периодич. часть, вообще говоря, не выделяется в виде прямого слагаемого. Периодич. А. г., порядки всех элементов к-рой являются степенями фиксированного простого числа р, наз. примарной по простому числу p(в общей теории групп употребляется термин р-группа). Всякая периодич. А. г. может быть разложена, притом единственным способом, в прямую сумму примерных групп, относящихся к различным простым числам. Наиболее полное описание известно для А. г. с конечным числом образующих. Его дает основная теорема об абелевых группах с конечным числом образующих: всякая конечно порожденная А. г. разлагается в прямую сумму конечного числа неразложимых циклич. подгрупп, из к-рых часть - конечные примарные, часть - бесконечные [Г. Фробениус (G. Frobenius), Л. Штиккельбергер (L. Stickelberger)]. В частности, конечная А. г. разложима в прямую сумму примарных циклич. групп. Такое разложение, вообще говоря, не единственно, но любые два разложения А. г. с конечным числом образующих в прямую сумму неразложимых циклич. групп изоморфны между собой и, таким образом, число бесконечных циклич. слагаемых и совокупность порядков примарных циклич. слагаемых не зависят от выбора разложения. Эти числа, наз. инвариантами конечно порожденной А. г., они являются полной системой инвариантов в том смысле, что всякие две группы, у к-рых эти инварианты совпадают, изоморфны. Всякая подгруппа А. г. с конечным числом образующих сама обладает конечной системой образующих. Не всякая А. г. представима в виде прямой суммы (даже бесконечного числа) циклич. групп. Для примарных А. г. имеется необходимое и достаточное условие существования такого разложения - критерий Куликова. Пусть А - примерная А. г. по нек-рому простому р. Ненулевой элемент агруппы Аназ. элементом бесконечной высоты в А, если для любого целого Конечное множество элементов Всякая А. г. без кручения ранга I изоморфна нек-рой подгруппе аддитивной группы рациональных чисел. Существует полное описание таких групп на языке типов. Всякому элементу А. г. без кручения ставится в соответствие его характеристика - счетная последовательность, состоящая из неотрицательных чисел и символа А. г. без кручения, разложимые в прямую сумму групп ранга I, наз. вполне разложимыми. Не всякая подгруппа вполне разложимой группы будет вполне разложимой (но всякое прямое слагаемое таково). Для всякого целого nсуществует А. г. без кручения ранга n, неразложимая в прямую сумму. Для счетных А. г. без кручения может быть построена полная система инвариантов. А. г. наз. полной, или делимой, если для любого ее элемента аи любого целого тв ней разрешимо уравнение Теория А. г., берущая свое начало в теории чисел, находит применение во многих современных математич. теориях. Так, теория двойственности характеров конечных А. г. получила глубокое развитие в теории двойственности для топологических локально компактных групп. Развитие гомологич. алгебры позволило решить ряд проблем в теории А. г., напр, дать описание множества всех расширений одной группы с помощью другой. Развитие теории модулей неразрывно связано с А. г. как модулями над кольцом целых чисел. Многие результаты теории А. г. удается перенести на случай модулей над кольцом главных идеалов. Относительная простота и изученность А. г. (что подтверждает, напр., разрешимость элементарной теории А. г.) вместе с довольно разнообразным запасом объектов делают А. г. постоянным источником примеров во многих разделах математики. |
|
|
|

 (или квазициклич. группы
(или квазициклич. группы  где
где  - произвольное простое число).
- произвольное простое число). уравнение
уравнение  разрешимо в А, и элементом высоты n, если это уравнение разрешимо лишь для
разрешимо в А, и элементом высоты n, если это уравнение разрешимо лишь для  Критерий Куликова: примерная А. г. разложима в прямую сумму циклич. групп тогда и только тогда, когда она есть объединение возрастающей последовательности своих подгрупп, у каждой из к-рых высоты элементов ограничены в совокупности. Любая подгруппа А. г., разложимой в прямую сумму циклич. подгрупп, сама разложима в прямую сумму циклич. подгрупп. Неразложимые (в прямую сумму) примарные группы исчерпываются циклич. примерными группами и группами
Критерий Куликова: примерная А. г. разложима в прямую сумму циклич. групп тогда и только тогда, когда она есть объединение возрастающей последовательности своих подгрупп, у каждой из к-рых высоты элементов ограничены в совокупности. Любая подгруппа А. г., разложимой в прямую сумму циклич. подгрупп, сама разложима в прямую сумму циклич. подгрупп. Неразложимые (в прямую сумму) примарные группы исчерпываются циклич. примерными группами и группами 
 А. г. наз. линейно зависимым, если существуют текие целые числа
А. г. наз. линейно зависимым, если существуют текие целые числа  не все равные нулю, что
не все равные нулю, что  Если же теких чисел не существует, то это множество наз. линейно независимым. Произвольная системе элементов А. г. наз. линейно зависимой, если линейно зависима нек-рая конечная ее подсистема. А. г., не являющаяся периодической, обладает максимальными линейно независимыми системами. Мощности всех максимальных линейно независимых подсистем одинаковы и наз. рангом (Прюфера) данной А. г. Ранг периодич. группы считается равным нулю. Ранг свободной А. г. совпадает с мощностью системы ее свободных образующих.
Если же теких чисел не существует, то это множество наз. линейно независимым. Произвольная системе элементов А. г. наз. линейно зависимой, если линейно зависима нек-рая конечная ее подсистема. А. г., не являющаяся периодической, обладает максимальными линейно независимыми системами. Мощности всех максимальных линейно независимых подсистем одинаковы и наз. рангом (Прюфера) данной А. г. Ранг периодич. группы считается равным нулю. Ранг свободной А. г. совпадает с мощностью системы ее свободных образующих.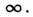 Эти последовательности строятся следующим образом. Все простые числа нумеруются в порядке возрастания
Эти последовательности строятся следующим образом. Все простые числа нумеруются в порядке возрастания 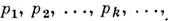 и элементу асопоставляется последовательность, на k-м месте к-рой стоит число
и элементу асопоставляется последовательность, на k-м месте к-рой стоит число 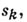 если уравнение
если уравнение  имеет решение в группе, а уравнение
имеет решение в группе, а уравнение  уже решения не имеет, и стоит символ
уже решения не имеет, и стоит символ  если уравнение
если уравнение  имеет решение при любом
имеет решение при любом  Характеристики считаются эквивалентными, если они отличаются не более, чем на конечном числе мест, и символ
Характеристики считаются эквивалентными, если они отличаются не более, чем на конечном числе мест, и символ  в каждой из них стоит на местах с одними и теми же номерами. Характеристики двух линейно зависимых элементов эквивалентны. Класс эквивалентных характеристик наз. типом. Всякой А. г. без кручения ранга I однозначно соответствует тип, наз. типом данной группы, причем неизоморфным группам соответствуют различные типы.
в каждой из них стоит на местах с одними и теми же номерами. Характеристики двух линейно зависимых элементов эквивалентны. Класс эквивалентных характеристик наз. типом. Всякой А. г. без кручения ранга I однозначно соответствует тип, наз. типом данной группы, причем неизоморфным группам соответствуют различные типы. Все делимые А. г. исчерпываются всевозможными прямыми суммами групп, изоморфных
Все делимые А. г. исчерпываются всевозможными прямыми суммами групп, изоморфных  и группам
и группам  причем мощности множеств компонент, изоморфных
причем мощности множеств компонент, изоморфных  а также
а также  (для каждого р), составляют полную и независимую систему инвариантов делимой группы. Всякая А. г. может быть изоморфно вложена в нек-рую делимую А. г. Делимые А. г. и только они являются инъективными объектами в категории А. г. и служат прямыми слагаемыми для всякой содержащей их А. г. Таким образом, всякая А. г. представима в виде прямой суммы полной группы и так наз. редуцированной группы, т. е. группы, к-рая не содержит ненулевых полных подгрупп. Описание редуцированных А. г. известно лишь в немногих случаях. Так, теорема Ульма (см. [1],
(для каждого р), составляют полную и независимую систему инвариантов делимой группы. Всякая А. г. может быть изоморфно вложена в нек-рую делимую А. г. Делимые А. г. и только они являются инъективными объектами в категории А. г. и служат прямыми слагаемыми для всякой содержащей их А. г. Таким образом, всякая А. г. представима в виде прямой суммы полной группы и так наз. редуцированной группы, т. е. группы, к-рая не содержит ненулевых полных подгрупп. Описание редуцированных А. г. известно лишь в немногих случаях. Так, теорема Ульма (см. [1],  28) дает описание всех счетных редуцированных периодич. А. г.
28) дает описание всех счетных редуцированных периодич. А. г.