|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ПЛОТНОСТНЫЙ МЕТОДЗначение ПЛОТНОСТНЫЙ МЕТОД в математической энциклопедии: - один из методов аналитич. теории чисел, основанный на изучении статистики распределения нулей дзета-функции Римана s=s+it - характер по модулю k. Многие теоретико-числовые проблемы получают наиболее законченное решение в предположении, что все нули r=b+ig функций z(s) и L(s,c), находящиеся в полосе Впервые П. м. с использованием плотностной теоремы для z(s) применил Г. Хоайзель (G. Hoheisel, 1930) для оценки разности двух соседних простых чисел. Ему удалось доказать существование положительной константы a<1 такой, что при х>х 0=х 0(a).между хи х+хa всегда находится простое число. В дальнейшем всякое улучшение оценки для N(s, Т).приводило к уточнению константы а. Для L-функции Дирихле П. м. был разработан Ю. В. Линником (1944 и последующие годы). Ю. В. Линник впервые исследовал распределение нулей L-функций при переменном k, в частности получил результаты о "частоте" нулей L(s,c) вблизи точки s=l, что позволило найти оценку для наименьшего простого числа p0=p0(k, l), лежащего в арифметич. прогрессии П. м. в теории L-функций позволил получить сильный результат в направлении бинарной проблемы Гольдбаха: всякое достаточно большое натуральное число можно представить в виде суммы двух простых чисел и ограниченного абсолютной константой нек-рого числа степеней двоек. Наиболее сильные результаты П. м. дает в сочетании с др. методами, в частности с методом большого решета. На этом пути была доказана теорема Виноградова - Бомбьери (1965), к-рая заменяет во многих случаях Римана обобщенную гипотезу. Идеи и результаты П. м. переносятся с поля рациональных чисел на поля алгебраич. чисел. Лит.:[1] Прахар К., Распределение простых чисел, пер. с нем., М., 1967; [2] Монтгомери Г., Мультипликативная теория чисел, пер. с англ., М., 1974; [3] НаIberstam H., Riсhеrt Н.- В., Sieve methods, L. -[а. о.], 1974. Б. М. Бредихин. |
|
|
|

 и L-функции Дирихле
и L-функции Дирихле 
 ,
,  , лежат на прямой s=1/2. Однако в ряде случаев достаточно сильные результаты получаются, если удается показать, что нули указанных функций с абсциссой
, лежат на прямой s=1/2. Однако в ряде случаев достаточно сильные результаты получаются, если удается показать, что нули указанных функций с абсциссой 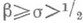 если и существуют, то все же составляют множество, к-рое становится все более редким при
если и существуют, то все же составляют множество, к-рое становится все более редким при  . Существует большое количество теорем, к-рые дают оценки сверху для числа N(s, Т).нулей z(s) и для числа N(s, Т,c) нулей L(s,c).в прямоугольнике
. Существует большое количество теорем, к-рые дают оценки сверху для числа N(s, Т).нулей z(s) и для числа N(s, Т,c) нулей L(s,c).в прямоугольнике  . П. м. существенно опирается на эти теоремы, получившие название плотностных теорем.
. П. м. существенно опирается на эти теоремы, получившие название плотностных теорем.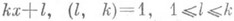 , х=0,1, 2, ... ; p0<kc, где с - нек-рая абсолютная константа. Улучшение оценок для
, х=0,1, 2, ... ; p0<kc, где с - нек-рая абсолютная константа. Улучшение оценок для  приводит к уточнению константы с. Применяя плотностные теоремы для L-функций, Ю. В. Линник нашел новое доказательство теоремы Виноградова о представлении всякого достаточно большого нечетного числа суммой трех простых чисел (см. Гольдбаха проблема).
приводит к уточнению константы с. Применяя плотностные теоремы для L-функций, Ю. В. Линник нашел новое доказательство теоремы Виноградова о представлении всякого достаточно большого нечетного числа суммой трех простых чисел (см. Гольдбаха проблема).