Математический словарь
|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ПЕТЕРСОНА - КОДАЦЦИ УРАВНЕНИЯЗначение ПЕТЕРСОНА - КОДАЦЦИ УРАВНЕНИЯ в математической энциклопедии: уравнения, составляющие вместе с уравнением Гаусса (см. Гаусса теорема).необходимые и достаточные условия интегрируемости системы, к к-рой сводится задача восстановления поверхности по ее первой и второй квадратичным формам (см. Бонне теорема). П. - К. у. имеют вид где bij- коэффициенты второй квадратичной формы, Уравнения впервые найдены К. М. Петерсоном в 1853, переоткрыты Г. Майнарди (G. Mainardi, 1856) и Д. Кодацци (D. Codazzi, 1867). Лит.:[1] Рашевский П. К., Курс дифференциальной геометрии, М., 1956. А. Б. Иванов. |
|
|
|

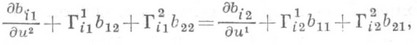
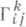 - символы Кристоффеля 2-го рода.
- символы Кристоффеля 2-го рода.