|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ПЕРРОНА - СТИЛТЬЕСА ИНТЕГРАЛЗначение ПЕРРОНА - СТИЛТЬЕСА ИНТЕГРАЛ в математической энциклопедии: обобщение понятия Перрона интеграла от функции одного действительного переменного. Конечная функция f(х).наз. интегрируемой в смысле Перрона - Стилтьеса относительно конечной функции G(х).на [ а, b], если на [а, b]существуют мажоранта М(х).и миноранта т(х).функции f(х).относительно G(x).на [а, b]с М(х)=т (а)=0 такие, что в каждой точке при всех достаточно малых Такое обобщение интеграла Перрона ввел О. Уорд Лит.:[1] Ward A. J., "Math. Z.", 1936, Bd 41, S. 578- 604; [2] Сакс С:, Теория интегрлла, пер. с англ., М., 1949; [3] Виноградова И. А., Скворцов В. А., в кн.: Математический анализ. 1970, М., 1971, с. 65-107. Т. П. Лукашенко. |
|
|
|
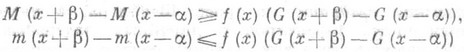
и 
, кроме того, нижняя грань чисел М(b), где М(х) - произвольная мажоранта f(х).относительно G(x), и верхняя грань чисел т(b), где т(х) - произвольная миноранта f(х).относительно G(x), равны между собой. Общее значение этих двух граней наз. П.-С. и. от f(х).относительно G(x).на [ а, b]и обозначается 