|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ПЕРИОДЗначение ПЕРИОД в математической энциклопедии: функции f(x) - число Числа + пТ, где п - любое натуральное число, также являются П. функции f(x). У функции f=const на оси или на плоскости любое число любое рациональное число где аи b - постоянные и Аналогично определяется П. функции, определенной на нек-рой абелевой группе. А. А. Конюшков. |
|
|
|

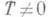 такое, что при любом
такое, что при любом 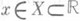 (или
(или  ) числа х-Т и x+Ттакже принадлежат множеству X и выполняется равенство
) числа х-Т и x+Ттакже принадлежат множеству X и выполняется равенство 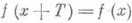
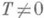 будет П.; для функции Дирихле
будет П.; для функции Дирихле 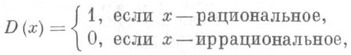
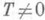 будет П. Если функция f(x).имеет период Т, то функция
будет П. Если функция f(x).имеет период Т, то функция 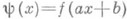 ,
, , имеет период
, имеет период 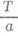 . Если действительная функция f(x). с действительным аргументом непрерывна на X(и не равна тождественно постоянной), то она имеет наименьший период T0>0 и всякий другой действительный П. кратен Т 0. Существуют функции с комплексным аргументом, у к-рых имеются два некратных с мнимым частным П.; таковы, напр., эллиптические функции.
. Если действительная функция f(x). с действительным аргументом непрерывна на X(и не равна тождественно постоянной), то она имеет наименьший период T0>0 и всякий другой действительный П. кратен Т 0. Существуют функции с комплексным аргументом, у к-рых имеются два некратных с мнимым частным П.; таковы, напр., эллиптические функции.