|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
БЕЙЕСОВСКИЙ ПОДХОДЗначение БЕЙЕСОВСКИЙ ПОДХОД в математической энциклопедии: к статистическим задачам - подход, основанный на предположении, что всякому параметру в статистич. проблеме принятия решения приписано нек-рое распределение вероятностей. Всякая общая статистич. проблема принятия решения определяется следующими элементами: пространством а
Таким образом, При отыскании бейесовской решающей функции Отсюда видно, что для данного или, что эквивалентно, где
Но по Бейеса формуле Тем самым для данного Тогда
откуда следует, что Преимущество Б. п. состоит в том, что полные потери
Недостатком Б. п. является необходимость постулировать как существование априорного распределения для неизвестного параметра, так и знание его формы (в определенной степени последнее обстоятельство преодолевается в рамках бейесовского подхода эмпирического). Лит.:[1] Вальд А., Статистические решающие функции, в сб.: Позиционные игры, М., 1967, с. 300-522; [2] Де Гроот М., Оптимальные статистические решения, пер. с англ., М., 1974. А. Н. Ширяев. |
|
|
|

 выборок
выборок  , пространством
, пространством  значений неизвестного параметра
значений неизвестного параметра  , семейством распределений вероятностей
, семейством распределений вероятностей  на
на  пространством решений
пространством решений  п функцией
п функцией  , характеризующей потери от принятия решения d, когда истинное значение параметра есть
, характеризующей потери от принятия решения d, когда истинное значение параметра есть  . Цель же проблемы принятия решения состоит в отыскании в определенном смысле наилучшего правила (решающей функции)
. Цель же проблемы принятия решения состоит в отыскании в определенном смысле наилучшего правила (решающей функции) , сопоставляющей каждому результату наблюдения .
, сопоставляющей каждому результату наблюдения . решение
решение  . При Б. п., когда считается, что неизвестный параметр 0 является случайной величиной с заданным (априорным) распределением
. При Б. п., когда считается, что неизвестный параметр 0 является случайной величиной с заданным (априорным) распределением  , наилучшая решающая функция (бейесовская решающая функция)
, наилучшая решающая функция (бейесовская решающая функция) определяется как функция, на к-рой достигаются минимальные полные потери
определяется как функция, на к-рой достигаются минимальные полные потери  , где
, где 


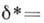
 полезным оказывается следующее замечание. Пусть
полезным оказывается следующее замечание. Пусть  где
где  и
и  - некоторые s-конечные меры. Тогда, предполагая возможным смену порядков интегрирования, находим
- некоторые s-конечные меры. Тогда, предполагая возможным смену порядков интегрирования, находим 
 есть то значение
есть то значение  , на к-ром достигается
, на к-ром достигается 



 есть то значение
есть то значение  , на к-ром достигают минимума условные средние потери
, на к-ром достигают минимума условные средние потери  .
.

 достигается на функции
достигается на функции 
 оказываются числом (в отличие от потерь
оказываются числом (в отличие от потерь  , зависящих от неизвестного параметра
, зависящих от неизвестного параметра  ), и, следовательно, заведомо существуют, если и не оптимальные, то, по крайней мере,
), и, следовательно, заведомо существуют, если и не оптимальные, то, по крайней мере,  -оптимальные (
-оптимальные ( ) решающие функции
) решающие функции  , для к-рых
, для к-рых