|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ПЕРЕСТАНОВКАЗначение ПЕРЕСТАНОВКА в математической энциклопедии: из пэлементов - конечная последовательность длины п, все элементы к-рой различны, т. е. П.- это размещение без повторения из пэлементов по п. Число перестановок равно п! Обычно в качестве элементов П. берут элементы множества Zn={1, 2, . .., п};взаимно однозначное отображение p множества Zn на себя определяет перестановку Примеры. 1) Пара (p(i), p(j)} образует в 2) Если bn - число таких перестановок Иногда П. наз. отображения в себя конечного множества, т. е. подстановки. Лит.:[1] Сачков В. Н. .Комбинаторные методы дискретной математики, М., 1977; [2] Риордан Д ж., Введение в комбинаторный анализ, пер. с англ., М., 1963. В. М. Михеев. |
|
|
|
. Отображение p наз. подстановкой Zn. Многие задачи, связанные с перечислением П., формулируются в терминах подстановок, как, напр., задачи о перечислении П. с различными ограничениями на позиции переставляемых элементов (см., напр., [1], [2]). Перестановка 
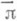может рассматриваться как упорядоченное множество, состоящее из пэлементов, если считать, что элемент p(i) предшествует элементу p(i+l), i=1, 2, . . ., п.
инверсию, если p(i)>p(j) при i<j. Если а r - число П. из пэлементов с r инверсиями, то 
из n элементов, что p(i)>p(i-1) при i четном и p(i)<p(i - 1) при iнечетном, то 