"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ПЕРЕСЕЧЕНИЯ ИНДЕКС
Значение ПЕРЕСЕЧЕНИЯ ИНДЕКС в математической энциклопедии:
- гомологический инвариант, характеризующий алгебраическое (т. е. учитывающее ориентацию) число точек пересечения двух подмножеств дополнительных размерностей в евклидовом пространстве или ориентированном многообразии (находящихся в общем положении). В случае неориентируемого многообразия в качестве кольца коэффициентов R для гомологии рассматривается  .
.
Пусть  - такие пары подмножеств евклидова пространства
- такие пары подмножеств евклидова пространства  , что
, что  , и пусть
, и пусть
 - отображение, для к-рого d(x,у)=х-у. Индексом пересечения xoh классов гомологии
- отображение, для к-рого d(x,у)=х-у. Индексом пересечения xoh классов гомологии  ,
, 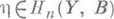 наз. элемент
наз. элемент  . Здесь d* - индуцированное отображение гомологии, а
. Здесь d* - индуцированное отображение гомологии, а
 - внешнее гомологич. произведение элементов xи h.
- внешнее гомологич. произведение элементов xи h.
П. и.  зависит лишь от тех частей классов x и т), носители к-рых попадают в произвольно малую окрестность Vзамыкания множества
зависит лишь от тех частей классов x и т), носители к-рых попадают в произвольно малую окрестность Vзамыкания множества  . В частности,
. В частности,  , если
, если  . Кроме того, если V
. Кроме того, если V ,
,  при
при  , то определены соответствующие каждому открытому множеству Vi локальные П. и. x и h), сумма к-рых совпадает с
, то определены соответствующие каждому открытому множеству Vi локальные П. и. x и h), сумма к-рых совпадает с  . Инвариант
. Инвариант  не меняется при гомеоморфизмах
не меняется при гомеоморфизмах  . Вместе с предшествующим свойством локальности это позволяет определить П. и.
. Вместе с предшествующим свойством локальности это позволяет определить П. и.  для компактных подмножеств ориентированного многообразия. Имеет место следующее соотношение антикоммутативности:
для компактных подмножеств ориентированного многообразия. Имеет место следующее соотношение антикоммутативности:

Если Xи Y- векторные подпространства общего положения,  а x и h - образующие
а x и h - образующие  , то
, то  - образующая
- образующая  . Так как выбор указанных образующих равносилен выбору ориентации в соответствующих евклидовых пространствах, это дает возможность определить П. и.
. Так как выбор указанных образующих равносилен выбору ориентации в соответствующих евклидовых пространствах, это дает возможность определить П. и.  двух цепей дополнительных размерностей (в том числе сингулярных), для к-рых
двух цепей дополнительных размерностей (в том числе сингулярных), для к-рых  (|с| - носитель, а дс - граница цепи с). При этом
(|с| - носитель, а дс - граница цепи с). При этом  для определяемых цепями с, с' классов гомологии
для определяемых цепями с, с' классов гомологии  ,
, 
П. и. применяется для описания нек-рых соотношений двойственности в многообразиях.
Лит.:[1] Дольд А., Лекции по алгебраической топологии, пер. с англ., М., 1076. Е. Г. Скляренко.

 .
. - такие пары подмножеств евклидова пространства
- такие пары подмножеств евклидова пространства  , что
, что  , и пусть
, и пусть  - отображение, для к-рого d(x,у)=х-у. Индексом пересечения xoh классов гомологии
- отображение, для к-рого d(x,у)=х-у. Индексом пересечения xoh классов гомологии  ,
, 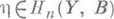 наз. элемент
наз. элемент  . Здесь d* - индуцированное отображение гомологии, а
. Здесь d* - индуцированное отображение гомологии, а  - внешнее гомологич. произведение элементов xи h.
- внешнее гомологич. произведение элементов xи h. зависит лишь от тех частей классов x и т), носители к-рых попадают в произвольно малую окрестность Vзамыкания множества
зависит лишь от тех частей классов x и т), носители к-рых попадают в произвольно малую окрестность Vзамыкания множества  . В частности,
. В частности,  , если
, если  . Кроме того, если V
. Кроме того, если V ,
,  при
при  , то определены соответствующие каждому открытому множеству Vi локальные П. и. x и h), сумма к-рых совпадает с
, то определены соответствующие каждому открытому множеству Vi локальные П. и. x и h), сумма к-рых совпадает с  . Инвариант
. Инвариант  не меняется при гомеоморфизмах
не меняется при гомеоморфизмах  . Вместе с предшествующим свойством локальности это позволяет определить П. и.
. Вместе с предшествующим свойством локальности это позволяет определить П. и.  для компактных подмножеств ориентированного многообразия. Имеет место следующее соотношение антикоммутативности:
для компактных подмножеств ориентированного многообразия. Имеет место следующее соотношение антикоммутативности:
 а x и h - образующие
а x и h - образующие  , то
, то  - образующая
- образующая  . Так как выбор указанных образующих равносилен выбору ориентации в соответствующих евклидовых пространствах, это дает возможность определить П. и.
. Так как выбор указанных образующих равносилен выбору ориентации в соответствующих евклидовых пространствах, это дает возможность определить П. и.  двух цепей дополнительных размерностей (в том числе сингулярных), для к-рых
двух цепей дополнительных размерностей (в том числе сингулярных), для к-рых  (|с| - носитель, а дс - граница цепи с). При этом
(|с| - носитель, а дс - граница цепи с). При этом  для определяемых цепями с, с' классов гомологии
для определяемых цепями с, с' классов гомологии  ,
, 