|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ПЕРВАЯ КВАДРАТИЧНАЯ ФОРМАЗначение ПЕРВАЯ КВАДРАТИЧНАЯ ФОРМА в математической энциклопедии: метрическая форма, поверхности - квадратичная форма от дифференциалов координат на поверхности, к-рая определяет внутреннюю геометрию поверхности в окрестности данной точки. Пусть поверхность задана уравнением где ии v - внутренние координаты на поверхности;
Квадрат главной линейной части приращения длины дуги ММ' выражается квадратом дифференциала dr: и наз. первой основной квадратичной формой поверхности. Коэффициенты П. к. ф. обычно обозначают через или в тензорных символах Тензор gij наз. основным, или метрическим, тензором поверхности. П. к. ф. является положительно определенной формой в обыкновенных точках поверхности: П. к. ф. характеризует метрич. свойства поверхности: знание П. к. ф. позволяет вычислять длины дуг на поверхности: где t - параметр на кривой; углы между кривыми на поверхности: где площади областей на поверхности: Вид коэффициентов П. К. ф. существенно зависит от выбора координат на поверхности. П. к. ф. имеет т. н. ортогональный вид: в ортогональных координатах; канонический в и д в полугеодезич. координатах; изотермический (изометрический) вид в изотермич. координатах, Иногда поверхности характеризуются специальными видами П. к. ф. Напр., Лиувилля поверхности характеризуются следующим видом П. к. ф.: П. к. ф. является инвариантом изгибания поверхности: полная кривизна поверхности в данной точке может быть вычислена через коэффициенты только П. к. ф. и их производные (теоремы Гаусса). О связи П. к. ф. с другими квадратичными формами поверхности и лит. см. в ст. Квадратичные формы поверхности. А. В. Иванов |
|
|
|


 - дифференциал радиус-вектора r вдоль выбранного направления du: dv смещения из точки Мв бесконечно близкую точку М' (см. рис. 1).
- дифференциал радиус-вектора r вдоль выбранного направления du: dv смещения из точки Мв бесконечно близкую точку М' (см. рис. 1). 






 и
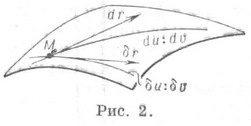
и  - направления векторов, касательных к кривым (см. рис. 2);
- направления векторов, касательных к кривым (см. рис. 2);