" 0 C F G H K L N P S T W Z А Б В Г Д Е Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш Э Ю Я

ПЕАНО ПРОИЗВОДНАЯ

Значение ПЕАНО ПРОИЗВОДНАЯ в математической энциклопедии:

- одно из обобщений понятия производной. Пусть существует d>0 такое, что для всех tс |t|<d имеет место

где - постоянные и при Пусть . Тогда число нав. обобщенной производной Пеано порядка rфункции f в точке х ₀. Обозначение: , в частности . Если существует f(r),(x₀), то существует и . Если существует конечная обычная двусторонняя производная , то . Обратное неверно при r>1: для функции

,

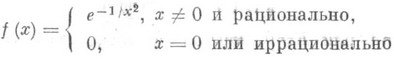имеет место , но не существует при (ибо f(x).разрывна при ). Следовательно, не существует обычная производная

при .

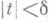Вводятся также и бесконечные обобщенные производные Пеано. Пусть для всех t с имеет место

где - постоянные и при ( - число или символ ). Тогда также наз. П. п. порядка rфункции f в точке x₀. Введена Дж. Пеано (G. Реаnо). А. А. Конюшков.