ПЕАНО КРИВАЯ

Значение ПЕАНО КРИВАЯ в математической энциклопедии:

- непрерывный образ отрезка, заполняющий внутренность квадрата (или треугольника). Открыта Дж. Пеано [1]. П. к., рассматриваемая как плоская фигура, не есть множество, нигде не плотное на плоскости; она является жордановой, но не канторовой кривой, а потому не является линией. Построение П. к., заполняющей квадрат, см. в ст. Линия;оно принадлежит Д. Гильберту (D. Hilbert). На рис. 1 приведен аналог его построения для треугольника (первые шесть шагов) (другие конструкции см. в [2] и [3]).

Всякая П. к. имеет кратные точки - это "предложение имеет огромную принципиальную важность для геометрии, так как оно показывает, в чем именно кроется самая геометрическая сущность различия числа измерений плоскости и прямой" (Н. Н. Лузин). Не существует П. к., всякая точка к-рой была бы простой или двукратной, но существует П. к., имеющая самое большее лишь трехкратные точки (в счетном числе), - такова, напр., кривая, построенная самим Дж. Пеано; конструкция Д. Гильберта содержит четырехкратные точки (также в счетном числе).

С понятием П. к. связан любопытный факт существования пространственных простых дуг, проектирующихся на плоскость в виде сплошных площадей,- такова, напр., кривая , где первые две функции задают П. к. Хотя эта, дуга и может служить непроницаемой для дождя крышей, однако она вовсе не есть непрерывная поверхность.

Известный интерес представляют т. н. правильные замкнутые кривые типа Пеано - пределы последовательностей симметричных замкнутых кривых, соответствующих последовательностям триангуляции произвольного правильного многоугольника, каждая из К-рых является правильным (т. е. полученным делением на Две равные части) подразделением предыдущей (пример - на рис. 2). При этом последовательность кривых можно выбрать так, чтобы предел площадей областей, ими ограниченных, был равен заданной величине (даже нулю или площади всей подразделяемой фигуры) (рис. 3). Кажется вероятным, что подобные картинки могут быть полезны при исследовании роста кристаллич. структур. Аналогично с помощью последовательностей триангуляции можно строить отображения прямой в плоскость, в частности "периодические" кривые типа Пеано.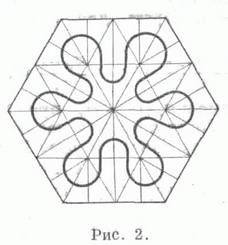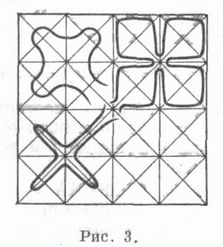

Существует аналог П. к., заполняющий многомерный и даже счетномерный куб (см. [3]).

Далеко идущее обобщение содержит теорема Мазуркевича ; если X - континуум, то эквивалентны условия: а) пространство Xлокально связно, б) X - непрерывный образ интервала.

Лит.:[1] Peano G., "Math. Ann.", 1890, Bd 36, S. 157; [2] Александров П. С., Введение в теорию множеств и общую топологию, М., 1877; [3] Лузин И. И., Теория функций действительного переменного, 2 изд., М., 1948.

М. И. Войцеховский.