|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ПАРАМЕТРИЧЕСКОЕ УРАВНЕНИЕЗначение ПАРАМЕТРИЧЕСКОЕ УРАВНЕНИЕ в математической энциклопедии: множества точек пространства - задание точек этого множества или их координат в виде значений функций нек-рых переменных, называемых параметрами. Параметрич. задание прямой в n-мерном векторном пространстве где x(0) и а - фиксированные векторы, х (0) - начальный вектор, а Параметрич. задание m-мерной гиперплоскости в Rn имеет вид где x(0) - начальный вектор, соответствующий нулевым значениям параметров tj,a a(1),...,а (m) - линейно независимая система твекторов, параллельных рассматриваемой гиперплоскости. В координатной форме уравнение (2) имеет вид Параметрич. задание m-мерной поверхности в где Е- напр., замыкание нек-рой области m-мерного пространства В качестве множества Е, на к-ром задано рассматриваемое параметрич. представление, иногда вместо замыкания m-мерной области берутся подмножества пространства |
|
|
|

 имеет вид
имеет вид 
 - направляющий вектор, параллельный прямой. Если в
- направляющий вектор, параллельный прямой. Если в  задан базис и координаты вектора хобозначаются через xl ,..., х n, то уравнение (1) в координатной форме имеет вид
задан базис и координаты вектора хобозначаются через xl ,..., х n, то уравнение (1) в координатной форме имеет вид 

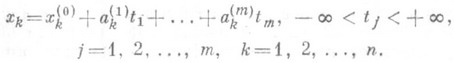
 имеет вид
имеет вид 
 , а
, а 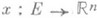 - отображение нек-рого класса: непрерывное, дифференцируемое, непрерывно дифференцируемое, дважды дифференцируемое и т. д., в зависимости от чего рассматриваемая m-мерная поверхность также наз. соответственно непрерывной, дифференцируемой и т. д. В случае m=1 множество Еявляется отрезком: Е=[ а, b]и П. у. (3) превращается в П. у. кривой: x=x(t),
- отображение нек-рого класса: непрерывное, дифференцируемое, непрерывно дифференцируемое, дважды дифференцируемое и т. д., в зависимости от чего рассматриваемая m-мерная поверхность также наз. соответственно непрерывной, дифференцируемой и т. д. В случае m=1 множество Еявляется отрезком: Е=[ а, b]и П. у. (3) превращается в П. у. кривой: x=x(t), , в пространстве
, в пространстве  . Напр., x1=cost, x2=sint,
. Напр., x1=cost, x2=sint,  , является П. у. на плоскости окружности единичного радиуса с центром в начале координат.
, является П. у. на плоскости окружности единичного радиуса с центром в начале координат. другой природы. л. д. Кудрявцев.
другой природы. л. д. Кудрявцев.