"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ПАРАМЕТРИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ
Значение ПАРАМЕТРИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ в математической энциклопедии:
в теории однолистных функций - представление однолистных функций, осуществляющих конформное отображение плоских областей на области канонич. вида (напр., на круг с концентрич. разрезами); оно возникает обычно следующим образом. Выбирается однопараметрич. семейство областей Qt,
 , вложенных друг в друга,
, вложенных друг в друга,  Для области Q0 предполагается известным ее конформное отображение
Для области Q0 предполагается известным ее конформное отображение  на нек-рую канонич. область В 0. По известному отображению
на нек-рую канонич. область В 0. По известному отображению  области
области  на область канонич. вида строится такое же отображение
на область канонич. вида строится такое же отображение  для области
для области 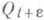 , где
, где  и мало. При непрерывном изменении параметра tна этом пути возникают дифференциальные уравнения, наиболее известными из к-рых являются Лёвнера уравнение и уравнение Лёвнера - Куфарева. В дискретном случае - для сеточных областей Qt и натурального параметра t - переход от отображения
и мало. При непрерывном изменении параметра tна этом пути возникают дифференциальные уравнения, наиболее известными из к-рых являются Лёвнера уравнение и уравнение Лёвнера - Куфарева. В дискретном случае - для сеточных областей Qt и натурального параметра t - переход от отображения 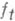 к отображению
к отображению  ,
,  , осуществляется по рекуррентным формулам. Источником упомянутых формул и уравнений служит обычно формула Шварца (см. [1] с. 92) и ее обобщения (см. [2]). Не менее важным источником П. п. служат вариации Адамара (см. [3], [4]) для функций Грина
, осуществляется по рекуррентным формулам. Источником упомянутых формул и уравнений служит обычно формула Шварца (см. [1] с. 92) и ее обобщения (см. [2]). Не менее важным источником П. п. служат вариации Адамара (см. [3], [4]) для функций Грина  , указанного выше семейства областей. Метод Адамара наз. также методом инвариантного погружения (см. [5]) для эллиптических дифференциальных уравнений. Ниже показана связь П. п., вариаций Адамара и инвариантного погружения в простейшем (дискретном) случае.
, указанного выше семейства областей. Метод Адамара наз. также методом инвариантного погружения (см. [5]) для эллиптических дифференциальных уравнений. Ниже показана связь П. п., вариаций Адамара и инвариантного погружения в простейшем (дискретном) случае.
Пусть Q - нек-рый набор целых комплексных чисел (сеточная область) и функция Грина  - экстремаль функционала Дирихле-Дугласа
- экстремаль функционала Дирихле-Дугласа

в классе П 0 всех действительных на Qфункций g(z). Здесь  ,
,
 (1)
(1)
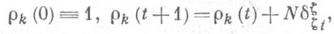
N- натуральное число,
 - символ Кронекера и zt=(kt, zt) t=0,1,..., Т-1,- нек-рый набор пар чисел; {zj|t=l,...,Т}- граница области Qt, kt=0 или 1. Нахождение экстремума функционала It(g) - задача квадратичного программирования. Сравнение ее решений при tи t+1 дает основную формулу инвариантного погружения (вариацию Адамара):
- символ Кронекера и zt=(kt, zt) t=0,1,..., Т-1,- нек-рый набор пар чисел; {zj|t=l,...,Т}- граница области Qt, kt=0 или 1. Нахождение экстремума функционала It(g) - задача квадратичного программирования. Сравнение ее решений при tи t+1 дает основную формулу инвариантного погружения (вариацию Адамара):
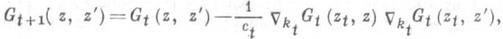
(2) где  символ
символ 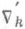 означает разностные операторы (1) по второму аргументу функции Грина. Зная функцию
означает разностные операторы (1) по второму аргументу функции Грина. Зная функцию  ,
,
можно шаг за шагом (рекуррентно) получить по формуле (2) все функции  .
.
Достроив функцию Грина до сеточно аналитич. ции 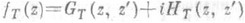 согласно уравнениям типа Коши - Римана
согласно уравнениям типа Коши - Римана

получают однолистное сеточно-квазиконформное отображение  области
области 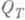 и единичный круг. Ближайшим к началу координат будет образ точки z'. В пределе при
и единичный круг. Ближайшим к началу координат будет образ точки z'. В пределе при  отображение сеточно-конформно и образом области
отображение сеточно-конформно и образом области 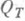 служит круг с концентрич. разрезами. Получен непрерывный аналог формулы (2) (см. [6]). В случае, когда все области
служит круг с концентрич. разрезами. Получен непрерывный аналог формулы (2) (см. [6]). В случае, когда все области 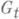 односвязны и канонич. областью служит единичный круг В, удается, используя дробно-линейные автоморфизмы круга В, представить функцию Грина в явном виде
односвязны и канонич. областью служит единичный круг В, удается, используя дробно-линейные автоморфизмы круга В, представить функцию Грина в явном виде
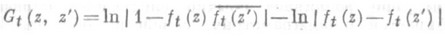
через функцию ft(z), отображающую Qt на В с нормировкой 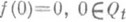 для всех
для всех 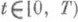
В терминах отображения w=ft(z) вариация Адамара сводится к обыкновенному дифференциальному уравнению (Лёвнера). По сравнению с вариацией Адамара это уравнение значительно проще, однако информация о границе области 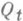 представлена в нем неявно - через управляющий параметр
представлена в нем неявно - через управляющий параметр 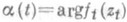 , поскольку функция
, поскольку функция 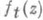 заранее неизвестна. Тем не менее уравнение Лёвнера - основной инструмент П. п.
заранее неизвестна. Тем не менее уравнение Лёвнера - основной инструмент П. п.
Были рассмотрены более общие однопараметрич. семейства областей  , не обязательно вложенных друг в друга (см. [7]). Возникающие при таких П. п. уравнения наз. уравнениями Куфарева - Лёвнера. Существуют также модификации уравнений Лёвнера и Куфарева - Лёвнера на те случаи, когда области
, не обязательно вложенных друг в друга (см. [7]). Возникающие при таких П. п. уравнения наз. уравнениями Куфарева - Лёвнера. Существуют также модификации уравнений Лёвнера и Куфарева - Лёвнера на те случаи, когда области 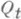 обладают различного рода симметриями или иными геометрич. особенностями (см. [1]). Лит.:[1] Голузин Г. М., Геометрическая теория функций комплексного переменного, 2 изд., М., 1966; [2] Александров. И. А., Сорокин А. С., "Сиб. матем. ж.", 1972, т. 13, № 5, с. 971 - 1001; [3] Hadamard J., Memoire sur le probleme d'analyse relatif a I'equilibri des plaques elastiques encastrees, P., 1908; [4] его же, Lecons sur le calcul des variations, v. 1, P., 1910; [5] Беллман Р., Энджел Э., Динамическое программирование и уравнения в частных производных, пер. с англ., М., 1974; [6] Попов В. И., "Докл. АН СССР", 1972, т. 207, № 5, с. 1048-50; [7] Куфарев П. П., "Матем. сб.", 1943, т. 13, № 1, с. 87-118. В. И. Попов.
обладают различного рода симметриями или иными геометрич. особенностями (см. [1]). Лит.:[1] Голузин Г. М., Геометрическая теория функций комплексного переменного, 2 изд., М., 1966; [2] Александров. И. А., Сорокин А. С., "Сиб. матем. ж.", 1972, т. 13, № 5, с. 971 - 1001; [3] Hadamard J., Memoire sur le probleme d'analyse relatif a I'equilibri des plaques elastiques encastrees, P., 1908; [4] его же, Lecons sur le calcul des variations, v. 1, P., 1910; [5] Беллман Р., Энджел Э., Динамическое программирование и уравнения в частных производных, пер. с англ., М., 1974; [6] Попов В. И., "Докл. АН СССР", 1972, т. 207, № 5, с. 1048-50; [7] Куфарев П. П., "Матем. сб.", 1943, т. 13, № 1, с. 87-118. В. И. Попов.

 , вложенных друг в друга,
, вложенных друг в друга,  Для области Q0 предполагается известным ее конформное отображение
Для области Q0 предполагается известным ее конформное отображение  на нек-рую канонич. область В 0. По известному отображению
на нек-рую канонич. область В 0. По известному отображению  области
области  на область канонич. вида строится такое же отображение
на область канонич. вида строится такое же отображение  для области
для области 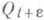 , где
, где  и мало. При непрерывном изменении параметра tна этом пути возникают дифференциальные уравнения, наиболее известными из к-рых являются Лёвнера уравнение и уравнение Лёвнера - Куфарева. В дискретном случае - для сеточных областей Qt и натурального параметра t - переход от отображения
и мало. При непрерывном изменении параметра tна этом пути возникают дифференциальные уравнения, наиболее известными из к-рых являются Лёвнера уравнение и уравнение Лёвнера - Куфарева. В дискретном случае - для сеточных областей Qt и натурального параметра t - переход от отображения 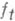 к отображению
к отображению  ,
,  , осуществляется по рекуррентным формулам. Источником упомянутых формул и уравнений служит обычно формула Шварца (см. [1] с. 92) и ее обобщения (см. [2]). Не менее важным источником П. п. служат вариации Адамара (см. [3], [4]) для функций Грина
, осуществляется по рекуррентным формулам. Источником упомянутых формул и уравнений служит обычно формула Шварца (см. [1] с. 92) и ее обобщения (см. [2]). Не менее важным источником П. п. служат вариации Адамара (см. [3], [4]) для функций Грина  , указанного выше семейства областей. Метод Адамара наз. также методом инвариантного погружения (см. [5]) для эллиптических дифференциальных уравнений. Ниже показана связь П. п., вариаций Адамара и инвариантного погружения в простейшем (дискретном) случае.
, указанного выше семейства областей. Метод Адамара наз. также методом инвариантного погружения (см. [5]) для эллиптических дифференциальных уравнений. Ниже показана связь П. п., вариаций Адамара и инвариантного погружения в простейшем (дискретном) случае. - экстремаль функционала Дирихле-Дугласа
- экстремаль функционала Дирихле-Дугласа 
 ,
, (1)
(1)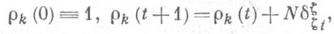
 - символ Кронекера и zt=(kt, zt) t=0,1,..., Т-1,- нек-рый набор пар чисел; {zj|t=l,...,Т}- граница области Qt, kt=0 или 1. Нахождение экстремума функционала It(g) - задача квадратичного программирования. Сравнение ее решений при tи t+1 дает основную формулу инвариантного погружения (вариацию Адамара):
- символ Кронекера и zt=(kt, zt) t=0,1,..., Т-1,- нек-рый набор пар чисел; {zj|t=l,...,Т}- граница области Qt, kt=0 или 1. Нахождение экстремума функционала It(g) - задача квадратичного программирования. Сравнение ее решений при tи t+1 дает основную формулу инвариантного погружения (вариацию Адамара):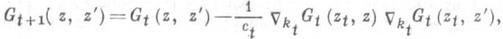
 символ
символ 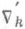 означает разностные операторы (1) по второму аргументу функции Грина. Зная функцию
означает разностные операторы (1) по второму аргументу функции Грина. Зная функцию  ,
, .
. 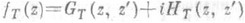 согласно уравнениям типа Коши - Римана
согласно уравнениям типа Коши - Римана 
 области
области 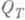 и единичный круг. Ближайшим к началу координат будет образ точки z'. В пределе при
и единичный круг. Ближайшим к началу координат будет образ точки z'. В пределе при  отображение сеточно-конформно и образом области
отображение сеточно-конформно и образом области 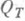 служит круг с концентрич. разрезами. Получен непрерывный аналог формулы (2) (см. [6]). В случае, когда все области
служит круг с концентрич. разрезами. Получен непрерывный аналог формулы (2) (см. [6]). В случае, когда все области 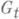 односвязны и канонич. областью служит единичный круг В, удается, используя дробно-линейные автоморфизмы круга В, представить функцию Грина в явном виде
односвязны и канонич. областью служит единичный круг В, удается, используя дробно-линейные автоморфизмы круга В, представить функцию Грина в явном виде 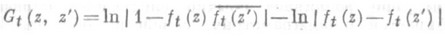
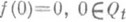 для всех
для всех 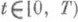
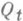 представлена в нем неявно - через управляющий параметр
представлена в нем неявно - через управляющий параметр 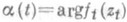 , поскольку функция
, поскольку функция 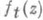 заранее неизвестна. Тем не менее уравнение Лёвнера - основной инструмент П. п.
заранее неизвестна. Тем не менее уравнение Лёвнера - основной инструмент П. п. , не обязательно вложенных друг в друга (см. [7]). Возникающие при таких П. п. уравнения наз. уравнениями Куфарева - Лёвнера. Существуют также модификации уравнений Лёвнера и Куфарева - Лёвнера на те случаи, когда области
, не обязательно вложенных друг в друга (см. [7]). Возникающие при таких П. п. уравнения наз. уравнениями Куфарева - Лёвнера. Существуют также модификации уравнений Лёвнера и Куфарева - Лёвнера на те случаи, когда области 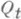 обладают различного рода симметриями или иными геометрич. особенностями (см. [1]). Лит.:[1] Голузин Г. М., Геометрическая теория функций комплексного переменного, 2 изд., М., 1966; [2] Александров. И. А., Сорокин А. С., "Сиб. матем. ж.", 1972, т. 13, № 5, с. 971 - 1001; [3] Hadamard J., Memoire sur le probleme d'analyse relatif a I'equilibri des plaques elastiques encastrees, P., 1908; [4] его же, Lecons sur le calcul des variations, v. 1, P., 1910; [5] Беллман Р., Энджел Э., Динамическое программирование и уравнения в частных производных, пер. с англ., М., 1974; [6] Попов В. И., "Докл. АН СССР", 1972, т. 207, № 5, с. 1048-50; [7] Куфарев П. П., "Матем. сб.", 1943, т. 13, № 1, с. 87-118. В. И. Попов.
обладают различного рода симметриями или иными геометрич. особенностями (см. [1]). Лит.:[1] Голузин Г. М., Геометрическая теория функций комплексного переменного, 2 изд., М., 1966; [2] Александров. И. А., Сорокин А. С., "Сиб. матем. ж.", 1972, т. 13, № 5, с. 971 - 1001; [3] Hadamard J., Memoire sur le probleme d'analyse relatif a I'equilibri des plaques elastiques encastrees, P., 1908; [4] его же, Lecons sur le calcul des variations, v. 1, P., 1910; [5] Беллман Р., Энджел Э., Динамическое программирование и уравнения в частных производных, пер. с англ., М., 1974; [6] Попов В. И., "Докл. АН СССР", 1972, т. 207, № 5, с. 1048-50; [7] Куфарев П. П., "Матем. сб.", 1943, т. 13, № 1, с. 87-118. В. И. Попов.