|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ОТРИЦАТЕЛЬНОЙ КРИВИЗНЫ ПОВЕРХНОСТЬЗначение ОТРИЦАТЕЛЬНОЙ КРИВИЗНЫ ПОВЕРХНОСТЬ в математической энциклопедии: в непосредственном понимании - Двумерная поверхность трехмерного евклидова пространства, к-рая в каждой своей точке имеет отрицательную гауссову кривизну К<0. Простейшие примеры: однополостный гиперболоид (рис. 1, а), гиперболический параболоид (рис. 1, б), катеноид. Непосредственное понимание О. к. п. можно обобщать, напр., по размерности самой поверхности или по размерности и по структуре объемлющего пространства. Локально О. к. п. имеют седловое строение. Это значит, что в достаточно малой окрестности любой своей точки О. к. п. похожа на седло (см. рис. 1, б, не интересуясь поведением поверхности вне изображенной ее части). Локальный седловой характер поверхности ясно усматривается на этом рисунке, где показаны главные сечения поверхности в произвольной точке О. Пусть гиперболоиды не прозрачны и их невидимые части (т. е. части любого из них, лежащие внутри другого) отброшены. Получившаяся поверхность имеет отрицательную кривизну всюду, кроме точек указанной гиперболы. В точках этой гиперболы кривизны вообще нет (в классическом понимании), т. к. гипербола является ребром поверхности. Но поверхность вблизи ребра в данном случае можно загладить [(см. [7]) так, чтобы получилась поверхность, к-рая имеет кривизну во всех точках, причем отрицательную (см. рис. 2, б). Она топологически эквивалентна тору с двумя проколами. Включая в конструкцию большее число однополостных гиперболоидов, можно построить О. к. п. сколь угодно сложного топологич. строения. Поверхность наз. полной, если она является полным метрич. пространством с расстоянием в смысле ее внутренней геометрии. Во всех указанных примерах рассматривались полные поверхности. Идея построения полных О. к. п. разнообразных топологич. типов, исходя из нек-рых простейших (как изложено выше), принадлежит Ж. Адамару (J. Hadamard, [1]). Предложен принципиально другой пример (рис. 3) полной О. к. п. (см. [6] - [7]). Эта поверхность имеет всюду отрицательную кривизну и вся заключена внутри нек-рого шара. Она бесконечно ветвится, причем переменная ее точка, двигаясь по ветвям, может сколь угодно близко подойти к граничной сфере шара, но нигде не достигает этой сферы. Поверхность построена так, что при указанном движении переменная точка всегда проходит путь бесконечной длины. Тем самым обеспечивается полнота поверхности в смысле ее внутренней метрики. Этот пример показывает, что внутренне полная О. к. п. не обязательно уходит в бесконечность в пространстве, подобно поверхностям в примерах Адамара. В приведенном примере повсеместное соблюдение условия К<0 удается обеспечить, допуская хотя бы слабую нерегулярность поверхности. Это значит, что поверхность предполагается гладкой (всюду класса С 1), но допускается, что в нек-рых изолированных точках она не принадлежит С 2; в таких точках требуется существование предельного значения кривизны. После дополнения предельными значениями кривизна всюду определена и непрерывна. Вопрос о протяженности поверхности и связь его с условием регулярности существенно дополняется следующими теоремами [8]. Если гауссова кривизна К полной поверхности класса С 2 удовлетворяет неравенству
Если на полной поверхности класса С 2, неограниченной во внутреннем смысле, гауссова кривизна Особое внимание привлекали (и привлекают) постоянной О. к. п., к-рые имеют гауссову кривизну с одним и тем же численным значением во всех точках. Они замечательны уже тем, что их внутренняя геометрия локально совпадает с геометрией на плоскости Лобачевского (см. Лобачевского геометрия). Это значит, что для фигур, лежащих на постоянной О. к. п., осуществляются в точности те же соотношения, какие имеют место в планиметрии Лобачевского (при этом роль прямых играют геодезич. линии); напр., тригонометрич. формулы для треугольников на постоянной О. к. п. и соответствующие формулы в неевклидовой геометрии Лобачевского точно совпадают. Тем самым на постоянной О. к. п. получается локальная модель геометрии Лобачевского. Такая модель была построена Э. Бельтрами (Е. Beltrami, 1868), что существенно содействовало признанию геометрии Лобачевского. Э. Бельтрами указал также важный пример О. к. п.; она наз. псевдосферой (рис. 4) и образована вращением трактрисы вокруг ее асимптоты (рис. 5). Характеристич. свойство трактрисы - отрезок касательной от точки прикосновения до асимптоты постоянно равен нек-рому числу а. Оказывается, что гауссова кривизна псевдосферы Еще раньше, чем Э. Бельтрами, поверхности вращения отрицательной кривизны изучал Ф. Миндинг (F. Minding, 1839). Он нашел два вида периодических постоянной О. к. п. вращения (рис. 6), к-рые вместе с псевдосферой исчерпывают все возможные постоянной О. к. п. (уравнения их см. в [3] и [5]).
Построение глобальной модели планиметрии Лобачевского на какой-нибудь постоянной О. к. п. вращения, напр. на псевдосфере, невозможно по двум причинам. Во-первых, на псевдосфере имеются нерегулярные точки; они составляют ребро возврата (рис. 4). Во-вторых, псевдосфера топологически эквивалентна трубке и значит даже с топологич. точки зрения отличается от плоскости Лобачевского. Но можно построить на регулярной О. к. п. вращения модель бесконечной части плоскости Лобачевского. С этой целью отсекается от псевдосферы плоскостью, перпендикулярной оси, бесконечная (сужающаяся) область U. Плоскость проводится так, чтобы она не содержала ребра возврата. В качестве Uберется та часть псевдосферы, где ребра возврата нет. Далее рассматривается только U, к-рую для простоты также наз. псевдосферой; на ней нет особых точек. Пусть U'- универсальная накрывающая псевдосферу Uповерхность. Это понятие можно наглядно ввести следующим образом. Берется бесконечно много одинаковых и совмещенных экземпляров псевдосферы U, к-рые различаются введением нумерации: На псевдосфере Uмеридианы, уходя в бесконечность, сближаются; кроме того, они ортогональны краю U. Поэтому край универсальной накрывающей есть кривая в плоскости Лобачевского, к-рая является ортогональной траекторией пучка параллельных по Лобачевскому (сближающихся) прямых. Эта кривая в геометрии Лобачевского наз. орициклом. Таким образом, с точки зрения своей внутренней геометрии универсальная накрывающая псевдосферы Uесть внутренняя область орицикла в плоскости Лобачевского. Универсальная накрывающая U' псевдосферы Uудобнее для построения модели геометрии Лобачевского, чем сама псевдосфера U. Напр., сколь угодно большой круг можно расположить на U', но в Uслишком большой круг без перекрытий может не уместиться. Но даже U' недостаточно обширна, чтобы вместить любой объект геометрии Лобачевского, напр. полная прямая в U' не умещается. Иначе говоря, построить с помощью U' модель всей плоскости Лобачевского нельзя. Д. Гильбертом (1900) был поставлен вопрос: не существует ли поверхности, внутренняя геометрия к-рой в целом совпадает с геометрией плоскости Лобачевского? Из простых соображений следует, что если такая поверхность есть, то она должна иметь постоянную отрицательную кривизну и быть полной. Далее, она должна быть односвязной, поскольку односвязна плоскость Лобачевского. Но на самом деле достаточно было бы найти любую полную поверхность постоянной отрицательной кривизны (согласно изложенному выше, универсальная накрывающая такой поверхности полна и односвязна). При этом имеются в виду только регулярные поверхности (хотя бы дважды непрерывно дифференцируемые в любой точке, т. е. класса С 2). Уже в 1901 Д. Гильберт решил свою проблему (см. [2]), причем в отрицательном смысле: в трехмерном евклидовом пространстве не существует полной регулярной поверхности постоянной отрицательной кривизны. Эта теорема привлекала внимание геометров на протяжении ряда десятилетий и привлекает внимание до сих пор. Дело в том, что с ней и с ее доказательством связано много интересных вопросов (см. ниже). При этом наличие особых линий у поверхностей вращения постоянной отрицательной кривизны (см. рис. 4, 6) не случайно. Оно соответствует теореме Гильберта. Доказательство теоремы Гильберта о поверхностях любого топологич. строения прежде всего интересно тем, что в нем существенно использовано понятие универсальной накрывающей поверхности. Оно сводит дело к поверхности с простейшей топологией, именно, к односвязной поверхности. По-видимому, теорема Гильберта была одним из ранних предложений математики, где это понятие уяснилось. После публикации первой статьи Д. Гильберта с доказательством его теоремы выражалось сомнение в справедливости этого доказательства. Замечания относились к необозримости поведения асимптотич. линий, к-рые по ходу дела рассматривались на поверхности ввиду сложности ре топологии. Предполагалось даже, что Д. Гильберт перерабатывал свое доказательство, чтобы уточнить его. Между тем доказательство Д. Гильберта с самого начала было безупречным. Вероятно, этих замечаний не было бы, если бы Д. Гильберт отчетливо сказал, что исследуется полное односвязное многообразие постоянной отрицательной кривизны, т. е. сама плоскость Лобачевского, в предположении, что она изометрично и регулярно погружена в трехмерное евклидово пространство. Интересным является также то, что в доказательстве Д. Гильберта неожиданно появляются чебышевские сети: так называется сеть, в каждом сетевом четырехугольнике к-рой противоположные стороны имеют равные длины (см. рис. 7). И вот оказывается, что асимптотич. сеть (к-рая определена и невырождена во всех точках на любой О. к. п.) в случае постоянной О. к. п.- чебышевская. Эту сеть можно принять в качестве координатной: u=const, v=const.
Тогда линейный элемент получает чебышевский вид где w - сетевой угол. Предполагая, что поверхность регулярна, полна и односвязна, и, пользуясь чебышевским характером сети, можно доказать, что и, v принимают все значения: при этом из геометрич. соображений следуют ограничения Д. Гильберт показал, что уравнение (2) не может иметь регулярного на все" координатной плоскости решения Во многих разделах математики случалось, что какое-нибудь утверждение или какой-нибудь вопрос играли особую роль в развитии всего раздела. В дифференциальной геометрии одним из таких утверждений была (и еще остается) теорема Гильберта. Ей посвящено много публикации. Интерес к этой теореме вызван прежде всего сочетанием в ее доказательстве разнообразных идей и понятий (универсального накрытия, чебышевской сети). Позднее обнаружилась ее связь с физикой. Оказалось, что уравнение (2), написанное в несколько ином виде и без ограничения (3), выражает условие на потенциал в т. н. эффекте Джозефсона из теории сверхпроводимости. Физики дали уравнению (2) название "синус-Гордона". Используя связь уравнения (2) с теорией О. к. п. (см. [13], [14]), находят в конечном виде нек-рые его решения, регулярные на всей плоскости. С. Э. Кон-Фоссен высказал (см. [15]) предположение, что имеет место гораздо более общая теорема, чем теорема Гильберта, именно, что условие на гауссову кривизну Для доказательства было найдено уравнение в случае переменной кривизны, к-рое обобщает уравнение (2). Именно, где w имеет прежний смысл, В случае переменной кривизны найдено (см. [17]) уравнение где - линейный оператор, пропорциональный оператору Здесь достаточна регулярность С 2. Но в случае Кроме (6) получены также (см. [21] ) другие равенства и оценки, универсальные в том смысле, что они относятся ко всем О. к. и. в Е 3. Кроме того, метод доказательства (6) позволил получить теоремы, к-рые дают достаточные признаки, когда отображение плоскости в плоскость с отрицательным якобианом является не только локальным, но и глобальным диффеоморфизмом. Несмотря на изложенные сейчас результаты, исследование (h,D)-метрик и других метрик с медленно изменяющейся кривизной (напр., q-метрик; см. [9]) не потеряло смысла. Дело в том, что в задачах погружения метрик с медленно изменяющейся отрицательной кривизной возникают эффекты, к-рые не имеют места в случае более общих метрик отрицательной кривизны (см., напр., теорему о простой зоне в [9]). Образно можно сказать, что чем медленнее изменяется кривизна, тем "труднее" метрике отрицательной кривизны быть погруженной в Е З. Для метрики постоянной кривизны это "явление" проявляется особенно заметно (см. усиленную теорему Гильберта в [9]). Что касается дифференциальных уравнений, к-рые отмечались в связи с вопросом о погружении (h,D)-метрик, то они существенно использовались и в других вопросах. Так, с их помощью установлен [7] ряд сильных теорем о связи между внутренними и внешними свойствами О. к. п.; в частности, теоремы о зависимости внешней регулярности кривизны О. к. п. -от регулярности ее метрики (см. 17]). Влияние регулярности метрики на внешнюю регулярность О. к. п. представляется особенно интересным, так как О. к. п. входят в нек-рый специальный класс поверхностей, к-рый может быть определен чисто геометрически (интересно, что чисто геометрия, определение допускает и класс выпуклых поверхностей). Поверхности этого класса наз. седловыми. Седловые поверхности в нек-ром смысле - антиподы выпуклых (см. [22] - [25]). Теорема о невозможности в евклидовом пространстве полной О. к. п. Пусть дана метрика ds2 с отрицательной гауссовой кривизной Ки Тогда основная система уравнений теории поверхностей примет симметричный вид где А 0,..., А г, выражаются только через метрику ds2. Выше указывалось, что полная О. к. п. с Построен пример односвязного многообразия знакопеременной кривизны, на к-ром есть геодезич. круг, не допускающий изометрич. погружения в Е 3 (см. [10]). Доказано [31] при нек-рых ограничениях на полную метрику односвязной О. к. п. Изучаются погружения метрики с гауссовой кривизной Разнообразие топологич. типов полных О. к. п. в Е 3 приводит к необходимости рассматривать различные подклассы этого слишком широкого класса, удовлетворяющие тем или иным дополнительным условиям. Весьма естественным является подкласс полных О. к. <п., имеющих взаимно однозначное сферическое ("однолистное") отображение (см. [33]). Если поверхность Fиз этого класса не имеет самопересечений, то она односвязна или двусвязна. Если такая поверхность Fимеет рог, то, используя неограниченность седлового рога (см. [34]), можно получить ряд внешнегеометрич. свойств этой поверхности: Fдопускает задание уравнением z=f(x,у).над областью, полученной из плоскости х, у удалением компактного выпуклого множества; F имеет предельный конус A(F), состоящий из луча, соответствующего рогу, и выпуклого конуса,, соответствующего чаше поверхности; замыкание
вопросов изучен и для других типов полных О. к. п. со взаимно однозначным сферич. отображением. Другим интересным по своим свойствам и свойствам своего сферич. отображения классом является класс сужающихся O.к. п. (см. [36], [37]). Такой поверхностью, напр., является поверхность, заданная уравнением Иначе выглядит теория О. к. п. в псевдоевклидовом пространстве Единичная сфера пространства О. к. п. с дефинитной метрикой образуют в Исчерпывающим образом изучены свойства поверхностей с дефинитной метрикой и отрицательной кривизной, полная интегральная кривизна к-рых кончена. Свойства этих поверхностей аналогичны свойствам выпуклых поверхностей с кривизной, меньшей 2p, в евклидовом пространстве (класс поверхностей Оловянишникова). Именно, полная дефинитная метрика отрицательной кривизны и конечной интегральной кривизны Полные О. к. п. с индефинитной метрикой также являются выпуклыми. Но свойства их отчасти сходны со свойствами седлообразных поверхностей в евклидовом пространстве. В частности, для них справедлива оценка sup K=0. Такие поверхности должны были бы соответствовать компоненте L3 единичной сферы пространства Лит.:[1] Нadamаrd J., "J. math, pures et appl.", 1898, v. 4, p. 27 - 73; [2] Hilbеrt D. "Trans. Amer. Math. Soc.", 1901, v. 2, p. 87-99; [3] Вianсhi L., Lezioni di geometria differentiate, 3 ed., v. 1, pt 1,.Bologna, 1927; [4] Ефимов Н. В., Высшая геометрия, 6 изд., М., 1978; Е5] Норден А. П., Теория поверхностей, М., 1956; [6] Розендорн Э. Р., "Успехи матем. наук", 1961, т. 16, в. 2, с. 149-56; [7] его же, там же, 1966, т. 21, в. 5, с. 59-116; [8] Аминов Ю. А.,"Укр. геометр, сб.", 1973, в. 13, с. 3-9; [9] Ефимов Н. В., "Успехи матем. наук", 1966, т. 21, в. 5, с. 3-58; [10] Позняк Э. Г., там же. 1973, т. 28, в. 4, с. 47-76; [11] Позняк Э. Г., Шикин Е. В., в кн.: Итоги науки и техники. Сер. Алгебра. Топология. Геометрия, т. 12, М., 1974, с. 171-207; [12] Позняк Э. Г., в кн.: Итоги науки и техники. Сер. Проблемы геометрии, т. 8, М., 1977, с. 225-41; [13] Грибков И. В., "Вести. Моск. ун-та. Сер. Математика. Механика", 1977, № 4, с. 78-83; [14] его же, "Успехи матем. наук", 1978, т. 33, в. 2, с. 191-92; [15] Конфоссен С. Э., там же, 1936, в. 1, с. 33-76; [16] Ефимов Н. В., "Докл. АН СССР", 1961, т. 136, Mi 6, с. 1283-86; [17] Ефимов Н. В., Позняк Э. Г., там же, т. 137, № 1, с. 25-27; [18] их же, там же, № 3, с. 509-12; [19] Е ф и-мо в Н. В., там же, 1963, т. 150, № 6, с. 1206-09; [20] его ж е, "Матем. сб.", 1964, т. 64, № 2, с. 286-320; [21] его же, там же, 1968, т. 76, №4, с. 499-512; [22] Шефель С. 3., Исследования по геометрии седловых поверхностей, Новосиб., 1963; [23] его же, "Сиб. матем. ж.", 1964, т. 5, № 6, с. 1382-96; [24] его же, там же, 1967, т. 8, JMi 3, с. 705-14; [25] его ж е, "Докл. АН СССР", 1965, т. 162, № 2, с. 294-96; [26] Ефимов Н. В., "Матем. сб.", 1976, т. 100, № 3, с. 356-63; [27] его же, "Докл. АН СССР", 1953, т. 93, М 4, с. 609-11; [28] Неinz Е., "Math. Ann.", 1955, Bd 129, Н. 5, p. 451-54; [29] Позняк Э. Г., "Докл. АН СССР", 1966, т. 170, № 4, с. 786 - 89; [30] его же, "Укр. геометр, сб.", 1966, в. 3, с. 78-92; [31] Шикин Е. В., "Докл. АН СССР", 1974, т. 215, № 1, с. 61-63; [32] Рождественский Б. Л., там же, 1962, т. 143, № 1, с. .10-52; [33] Вернер А. Л., "Матем. сб.", 1967, т. 74, № 2, с. 218-40; 1968, т. 75, № 1, с. 112-39, т. 77, № 1, с. 136; [34] его ж е, "Сиб. матем. ж.", 1970, т. 11, № 1, с. 20-29; № 4, с. 750- 769; [35] его же, "Матем. заметки", 1972, т. 12, № 3, с. 281-86; [36] Соколов Д. Д., "Успехи матем. наук", 1975, т. 30, в. 1, с. 261-62; 1978, т. 33, в. 4, с. 227 - 28; 1979, т. 34, в. 3, с. 213-14; [37] Александров А. Д., Внутренняя геометрии выпуклых поверхностей, М.--Л., 1948; [38] IIогорелов А. В., Внешняя геометрия выпуклых поверхностей, М., 1969. Н. В. Ефимов. |
|
|
|



 - их нормальные кривизны, т. е. главные кривизны в точке О. По классич. определению, гауссова кривизна в точке Оесть число
- их нормальные кривизны, т. е. главные кривизны в точке О. По классич. определению, гауссова кривизна в точке Оесть число  . Так как K<0, то главные кривизны имеют разные знаки, поэтому главные сечения имеют противоположные направления выпуклости; на рис. 1,б выпуклость сечения О2 направлена по нормали п, выпуклость другого - против нормали, что и соответствует седловому характеру поверхности. Топологич. строение О. к. п. в целом ("глобальное") может быть весьма разнообразным. Напр., гиперболич. параболоид (рис. 1, б) топологически эквивалентен плоскости, однополостный гиперболоид (рис. 1, а) - цилиндрич. трубке. Пусть два однополостных гиперболоида с параллельными осями пересекаются по гиперболе (рис. 2, а). Пусть эти
. Так как K<0, то главные кривизны имеют разные знаки, поэтому главные сечения имеют противоположные направления выпуклости; на рис. 1,б выпуклость сечения О2 направлена по нормали п, выпуклость другого - против нормали, что и соответствует седловому характеру поверхности. Топологич. строение О. к. п. в целом ("глобальное") может быть весьма разнообразным. Напр., гиперболич. параболоид (рис. 1, б) топологически эквивалентен плоскости, однополостный гиперболоид (рис. 1, а) - цилиндрич. трубке. Пусть два однополостных гиперболоида с параллельными осями пересекаются по гиперболе (рис. 2, а). Пусть эти 

 , где a=const, то поверхность не может содержаться в шаре, радиус к-рого меньше
, где a=const, то поверхность не может содержаться в шаре, радиус к-рого меньше 
 на бесконечности, то поверхность не ограничена в пространстве (в этой теореме допускается перемена знака кривизны).
на бесконечности, то поверхность не ограничена в пространстве (в этой теореме допускается перемена знака кривизны). .
. 


 Затем все они разрезаются по какому-нибудь общему меридиану, а на каждой из них устанавливается левый и правый берег разреза так, чтобы все левые берега были совмещены (также - правые). Теперь для любого номера
Затем все они разрезаются по какому-нибудь общему меридиану, а на каждой из них устанавливается левый и правый берег разреза так, чтобы все левые берега были совмещены (также - правые). Теперь для любого номера  левый берег Uk, соединяется с правым берегом Uk+1 (следовательно, правый берег Uk с левым берегом Uk-1). Так получится связная поверхность U', к-рая и является универсальной накрывающей поверхности U, она иногда наз. односвязной оберткой поверхности U. Универсальную накрывающую можно построить для любой поверхности, но наглядное описание ее конструкции будет далеко не так просто, как для псевдосферы. Существенно, что универсальная накрывающая всегда односвязна. Важно также, что на универсальную накрывающую можно перенести локальную внутреннюю геометрию накрываемой поверхности. Для этого достаточно учесть, что каждая точка р накрываемой поверхности имеет выпуклую окрестность V(p), к-рая однолистно накрывается окрестностью V'( р ').накрывающей (здесь р' -точка, к-рая накрывает точку р;соответствие
левый берег Uk, соединяется с правым берегом Uk+1 (следовательно, правый берег Uk с левым берегом Uk-1). Так получится связная поверхность U', к-рая и является универсальной накрывающей поверхности U, она иногда наз. односвязной оберткой поверхности U. Универсальную накрывающую можно построить для любой поверхности, но наглядное описание ее конструкции будет далеко не так просто, как для псевдосферы. Существенно, что универсальная накрывающая всегда односвязна. Важно также, что на универсальную накрывающую можно перенести локальную внутреннюю геометрию накрываемой поверхности. Для этого достаточно учесть, что каждая точка р накрываемой поверхности имеет выпуклую окрестность V(p), к-рая однолистно накрывается окрестностью V'( р ').накрывающей (здесь р' -точка, к-рая накрывает точку р;соответствие  биективно). Геометрия V(p).переносится на V'(p') тождественно, т. е. расстояние между точками
биективно). Геометрия V(p).переносится на V'(p') тождественно, т. е. расстояние между точками  принимается равным расстоянию между их прообразами. Вместе с тем определяется глобальная геометрия универсальной накрывающей, но она, как правило, будет совершенно отличаться от глобальной геометрии накрываемой.
принимается равным расстоянию между их прообразами. Вместе с тем определяется глобальная геометрия универсальной накрывающей, но она, как правило, будет совершенно отличаться от глобальной геометрии накрываемой.

 и этим исчерпывают сеть; иначе говоря, асимптотич. сеть в целом гомеоморфна декартовой сети на евклидовой координатной плоскости (см. [9]). С другой стороны, в предположении, что гауссова кривизна постоянна, напр. К=-1, из (1) получается уравнение
и этим исчерпывают сеть; иначе говоря, асимптотич. сеть в целом гомеоморфна декартовой сети на евклидовой координатной плоскости (см. [9]). С другой стороны, в предположении, что гауссова кривизна постоянна, напр. К=-1, из (1) получается уравнение 

 , подчиненного условию (3), и тем самым полная плоскость Лобачевского не может быть регулярно и изометрично погружена в трехмерное евклидово пространство. Отсюда, как объяснялось выше, вытекает более общая формулировка этой теоремы: в трехмерном евклидовом пространстве невозможна полная регулярная постоянной О. к. п. (никакой топологич. структуры).
, подчиненного условию (3), и тем самым полная плоскость Лобачевского не может быть регулярно и изометрично погружена в трехмерное евклидово пространство. Отсюда, как объяснялось выше, вытекает более общая формулировка этой теоремы: в трехмерном евклидовом пространстве невозможна полная регулярная постоянной О. к. п. (никакой топологич. структуры). можно заменить условием K
можно заменить условием K . Однако до нач. 60-х гг. 20 в. не было найдено ни одной теоремы, к-рая включала бы теорему Гильберта как частный случай. Только в 1961 (см. [16]) была доказана корректность теоремы Гильберта, т. е. была установлена теорема о переменной О. к. п., для к-рой теорема Гильберта является предельным случаем. Иначе говоря, те свойства постоянной О. к. п., к-рые вызывают эффект теоремы Гильберта (нарушение регулярности), и сам эффект возможно понимать в приближенном смысле.
. Однако до нач. 60-х гг. 20 в. не было найдено ни одной теоремы, к-рая включала бы теорему Гильберта как частный случай. Только в 1961 (см. [16]) была доказана корректность теоремы Гильберта, т. е. была установлена теорема о переменной О. к. п., для к-рой теорема Гильберта является предельным случаем. Иначе говоря, те свойства постоянной О. к. п., к-рые вызывают эффект теоремы Гильберта (нарушение регулярности), и сам эффект возможно понимать в приближенном смысле. 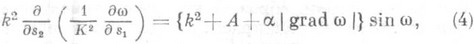
 , дифференцирование ведется по дугам асимптотич. линий, А и а, - величины, модули к-рых допускают внутреннюю оценку, т. е. оценку в зависимости только от погружаемой метрики. При К=const получается А=0,a=О и уравнение (4) превращается в уравнение (2).
, дифференцирование ведется по дугам асимптотич. линий, А и а, - величины, модули к-рых допускают внутреннюю оценку, т. е. оценку в зависимости только от погружаемой метрики. При К=const получается А=0,a=О и уравнение (4) превращается в уравнение (2).
 дифференцирования по дуге асимптотич. линий второго семейства,
дифференцирования по дуге асимптотич. линий второго семейства,  - квазилинейный оператор похожей структуры. Существенно, что функция Мпри нек-рых условиях на метрику допускает внутреннюю оценку снизу положительным числом, благодаря чему и благодаря строению левой части уравнение (5) сходно с уравнением (2). Поэтому при таких условиях наметрику можно провести рассуждения, сходные с рассуждениями Д. Гильберта (хотя гораздо более сложные), и получить сходный результат. Таким путем впервые было получено обобщение теоремы Гильберта (см. [18]). Что касается условий на метрику, о к-рых только что говорилось, то они заключаются в требовании, чтобы гауссова кривизна Л" была отгорожена от нуля и медленно изменялась. Если предположить, что
- квазилинейный оператор похожей структуры. Существенно, что функция Мпри нек-рых условиях на метрику допускает внутреннюю оценку снизу положительным числом, благодаря чему и благодаря строению левой части уравнение (5) сходно с уравнением (2). Поэтому при таких условиях наметрику можно провести рассуждения, сходные с рассуждениями Д. Гильберта (хотя гораздо более сложные), и получить сходный результат. Таким путем впервые было получено обобщение теоремы Гильберта (см. [18]). Что касается условий на метрику, о к-рых только что говорилось, то они заключаются в требовании, чтобы гауссова кривизна Л" была отгорожена от нуля и медленно изменялась. Если предположить, что  , то медленное изменение кривизны нужно понимать в том смысле, что первые и вторые производные от Кпо дуге любой геодезической достаточно малы. Достаточные оценки устанавливаются с таким расчетом, чтобы к уравнению (5).были применены указанные выше рассуждения, идущие от Д. Гильберта. Эти оценки (см. [19]) выражены с помощью положительных постоянных, обозначаемых hи a. Соответственно, получаемые метрики с медленно изменяющейся отрицательной кривизной наз. (h, D) - метриками (определение см. в [18] или в [19]); при этом метрики постоянной кривизны получаются при
, то медленное изменение кривизны нужно понимать в том смысле, что первые и вторые производные от Кпо дуге любой геодезической достаточно малы. Достаточные оценки устанавливаются с таким расчетом, чтобы к уравнению (5).были применены указанные выше рассуждения, идущие от Д. Гильберта. Эти оценки (см. [19]) выражены с помощью положительных постоянных, обозначаемых hи a. Соответственно, получаемые метрики с медленно изменяющейся отрицательной кривизной наз. (h, D) - метриками (определение см. в [18] или в [19]); при этом метрики постоянной кривизны получаются при  . Таким образом, полная (h,D) - метрика не допускает регулярного изометрич. погружения в трехмерное евклидово пространство. Вопрос о возможности обобщения теоремы Гильберта в том виде, как он ставился в 30-е гг. (без ограничений характера поведения кривизны, см. [12]), на указанных сейчас путях, т. е. с помощью дифференциальных уравнений теории поверхностей, завершить не удалось. Но решение этого вопроса получилось совсем на другом пути, именно, с помощью тщательного исследования граничных свойств сферич. образа О. к. п. Таким способом доказано (см. [19], [20]), что полная метрика с гауссовой кривизной
. Таким образом, полная (h,D) - метрика не допускает регулярного изометрич. погружения в трехмерное евклидово пространство. Вопрос о возможности обобщения теоремы Гильберта в том виде, как он ставился в 30-е гг. (без ограничений характера поведения кривизны, см. [12]), на указанных сейчас путях, т. е. с помощью дифференциальных уравнений теории поверхностей, завершить не удалось. Но решение этого вопроса получилось совсем на другом пути, именно, с помощью тщательного исследования граничных свойств сферич. образа О. к. п. Таким способом доказано (см. [19], [20]), что полная метрика с гауссовой кривизной  не допускает регулярного изометрич. погружения в Е 3. Тем самым вопрос решен точно в классич. постановке. Одновременно доказана теорема: в Е 3 на всякой полной регулярной поверхности отрицательной гауссовой кривизны Кимеет место равенство
не допускает регулярного изометрич. погружения в Е 3. Тем самым вопрос решен точно в классич. постановке. Одновременно доказана теорема: в Е 3 на всякой полной регулярной поверхности отрицательной гауссовой кривизны Кимеет место равенство  (6)
(6) есть (см. [7]) контрпример (в виде слабо нерегулярной поверхности).
есть (см. [7]) контрпример (в виде слабо нерегулярной поверхности). получает весьма усиленную форму в случае поверхности, к-рая однолистно проектируется на плоскость, т. е. может быть представлена как график функции
получает весьма усиленную форму в случае поверхности, к-рая однолистно проектируется на плоскость, т. е. может быть представлена как график функции  . В этом случае существуют универсальные оценки протяженности поверхности, и полнота ее становится несущественной. Доказаны теоремы (см. [26]): 1) если на прямоугольник со сторонами а, bрегулярно проектируется поверхность с гауссовой кривизной
. В этом случае существуют универсальные оценки протяженности поверхности, и полнота ее становится несущественной. Доказаны теоремы (см. [26]): 1) если на прямоугольник со сторонами а, bрегулярно проектируется поверхность с гауссовой кривизной  , то неравенство
, то неравенство  влечет
влечет  , где С 1, С 2- универсальные постоянные (напр., C1=4p, С 2=12p); 2) если а, b и (для простоты) a=1, то
, где С 1, С 2- универсальные постоянные (напр., C1=4p, С 2=12p); 2) если а, b и (для простоты) a=1, то 
 . Пусть метрика ds2 погружена в Е 3 и l, т, п - приведенные коэффициенты получившейся второй квадратичной формы (приведенные - значит удовлетворяющие уравнению ln-т 2= -К). В задаче о погружении l, т, п - неизвестные функции. В качестве новых неизвестных функций вводятся т. н. инварианты Римана:
. Пусть метрика ds2 погружена в Е 3 и l, т, п - приведенные коэффициенты получившейся второй квадратичной формы (приведенные - значит удовлетворяющие уравнению ln-т 2= -К). В задаче о погружении l, т, п - неизвестные функции. В качестве новых неизвестных функций вводятся т. н. инварианты Римана:

 не допускает изометричного регулярного погружения в Е 0. Поэтому полученные результаты о возможности изометрич. погружения двумерных многообразий отрицательной кривизны в Е 3 по необходимости относятся к частям полных многообразии. Само многообразие предполагается односвязным. Так, доказано (см. [29], [30]), что каждый геодезич. круг на произвольном регулярном многообразии отрицательней кривизны
не допускает изометричного регулярного погружения в Е 0. Поэтому полученные результаты о возможности изометрич. погружения двумерных многообразий отрицательной кривизны в Е 3 по необходимости относятся к частям полных многообразии. Само многообразие предполагается односвязным. Так, доказано (см. [29], [30]), что каждый геодезич. круг на произвольном регулярном многообразии отрицательней кривизны  может быть регулярно изометрически погружен в E3. Эта теорема получена как следствие более общей теоремы: при нек-рых естественных условиях регулярности на метрику полной О. к. п. с K
может быть регулярно изометрически погружен в E3. Эта теорема получена как следствие более общей теоремы: при нек-рых естественных условиях регулярности на метрику полной О. к. п. с K каждая бесконечная эквидистантная полоса на зтом многообразии может быть изометрично и регулярно погружена в Е 3. Эта теорема в свою очередь получена как следствие теоремы о существовании п целом решений гиперболич. систем квазилинейных уравнений вида (7), причем
каждая бесконечная эквидистантная полоса на зтом многообразии может быть изометрично и регулярно погружена в Е 3. Эта теорема в свою очередь получена как следствие теоремы о существовании п целом решений гиперболич. систем квазилинейных уравнений вида (7), причем  .
. , что внутренняя область произвольного орицикла такого многообразия может быть изометрично погружена в Е 3. Таким образом, для полных односвязных многообразий отрицательной кривизны
, что внутренняя область произвольного орицикла такого многообразия может быть изометрично погружена в Е 3. Таким образом, для полных односвязных многообразий отрицательной кривизны  доказана возможность изометрич. погружения в Е 3 всех компактных и некомпактных его частей, к-рые сходны с частями плоскости Лобачевского, изометрич. погружения к-рых известны из работ Ф. Миндинга и Э. Бельтрами.
доказана возможность изометрич. погружения в Е 3 всех компактных и некомпактных его частей, к-рые сходны с частями плоскости Лобачевского, изометрич. погружения к-рых известны из работ Ф. Миндинга и Э. Бельтрами. , т. е. погружения частей плоскости Лобачевского. Так, доказано, что каждый, даже бесконечно протяженный, многоугольник плоскости Лобачевского, может быть изометрически погружен в Е 3.
, т. е. погружения частей плоскости Лобачевского. Так, доказано, что каждый, даже бесконечно протяженный, многоугольник плоскости Лобачевского, может быть изометрически погружен в Е 3. сферич. образа поверхности Fимеет своим дополнением до сферы открытую полусферу и открытое выпуклое множество (рис. 8-10). Ряд аналогичных
сферич. образа поверхности Fимеет своим дополнением до сферы открытую полусферу и открытое выпуклое множество (рис. 8-10). Ряд аналогичных 


 . По ряду своих свойств сужающиеся О. к. п. напоминают замкнутые поверхности. Их сферич. образ можно рассматривать как ри-манову поверхность с краем, каждая компонента к-рого является сферич. ломаной, лежащей на одной из больших окружностей.
. По ряду своих свойств сужающиеся О. к. п. напоминают замкнутые поверхности. Их сферич. образ можно рассматривать как ри-манову поверхность с краем, каждая компонента к-рого является сферич. ломаной, лежащей на одной из больших окружностей. . В этом пространстве О. к. п. являются выпуклыми; при этом кривизна понимается обычным образом, как кривизна метрики, индуцированной объемлющим пространством. Именно она предполагается отрицательной.
. В этом пространстве О. к. п. являются выпуклыми; при этом кривизна понимается обычным образом, как кривизна метрики, индуцированной объемлющим пространством. Именно она предполагается отрицательной. состоит из трех связных компонент L1 L2, L3 (рис. 11). Компоненты L1 и L2 являются выпуклыми поверхностями, на к-рых индуцируется положительно определенная метрика постоянной отрицательной кривизны; эти поверхности дают известную интерпретацию геометрии Лобачевского. Поверхность L3 седлообразная, на ней индуцируется индефинитная метрика постоянной положительной кривизны; метрика этой поверхности известна как двумерная метрика де Ситтера.
состоит из трех связных компонент L1 L2, L3 (рис. 11). Компоненты L1 и L2 являются выпуклыми поверхностями, на к-рых индуцируется положительно определенная метрика постоянной отрицательной кривизны; эти поверхности дают известную интерпретацию геометрии Лобачевского. Поверхность L3 седлообразная, на ней индуцируется индефинитная метрика постоянной положительной кривизны; метрика этой поверхности известна как двумерная метрика де Ситтера.
 широкий и естественный класс поверхностей, обобщающих свойства поверхностей L1 и L2 так же, как поверхности положительной кривизны образуют в евклидовом пространстве класс, обобщающий сферу (см. [38]).
широкий и естественный класс поверхностей, обобщающих свойства поверхностей L1 и L2 так же, как поверхности положительной кривизны образуют в евклидовом пространстве класс, обобщающий сферу (см. [38]). и геодезич. луч g на многообразии, несущем эту метрику, определяют единственным образом выпуклую поверхность с данным выпуклым предельным конусом полной кривизны
и геодезич. луч g на многообразии, несущем эту метрику, определяют единственным образом выпуклую поверхность с данным выпуклым предельным конусом полной кривизны  без изотропных образующих и с данной образующей, к-рая является предельной для луча g. Регулярность получаемых поверхностей определяется регулярностью метрики.
без изотропных образующих и с данной образующей, к-рая является предельной для луча g. Регулярность получаемых поверхностей определяется регулярностью метрики. ; однако она не выпукла. Здесь играет определяющую роль не только знак гауссовой кривизны, но и знак определителя метрич. формы поверхности.
; однако она не выпукла. Здесь играет определяющую роль не только знак гауссовой кривизны, но и знак определителя метрич. формы поверхности.