|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
БЕЗГРАНИЧНО ДЕЛИМОЕ РАСПРЕДЕЛЕНИЕЗначение БЕЗГРАНИЧНО ДЕЛИМОЕ РАСПРЕДЕЛЕНИЕ в математической энциклопедии: распределение вероятностей, к-рое при любом п=2,3, 4, ... может быть представлено как композиция (свертка) подинаковых распределений вероятностей. Определение Б. д. р. в равной степени применимо к распределениям на прямой, в конечномерных евклидовых пространствах и в нек-рых еще более общих случаях. Ниже рассматривается одномерный случай. Характеристич. функции f(t).В. д. р. наз. безгранично делимыми. Каждая такая функция при любом пможет быть представлена как n-я степень некоторой другой характеристич. функции: Примерами Б. д. р. могут служить нормальное распределение, Пуассона распределение, Коши распределение, "хu-квадрат" распределение. Проверять свойство безграничной делимости проще всего с помощью характеристич. функций. Композиция Б. д. р. и предел слабо сходящейся последовательности Б. д. р. суть снова Б. д. р. Случайную величину, определенную на нек-ром вероятностном пространстве, наз. безгранично делимой, если при любом пона может быть представлена в виде суммы пнезависимых одинаково распределенных случайных величин, определенных на том же пространстве. Распределение каждой такой величины - Б. д. р. Обратное не всегда верно. Так, если взять дискретное вероятностное пространство, образованное неотрицательными целыми числами m=0, 1, 2, ... с приписанными им пуассоновскими вероятностями то случайная величина Б. д. р. впервые появились в связи с изучением стохастически непрерывных однородных случайных процессов с независимыми приращениями (см. [1], [2], [3]). Так называют процессы являются взаимно независимыми случайными величинами; 4) для любого при Общий вид Характеристич. функция Б. д. р. нигде не обращается в нуль, и ее логарифм (в смысле главного значения) допускает представление вида: (так наз. каноническое представление Леви- Хинчина), где Тогда для нормального распределения с математич. ожиданием Для распределения Пуассона с параметром
Для распределения Коши с плотностью имеем
Канонич. представление (*) удобно с чисто "технической" точки зрения (благодаря тому, что Gимеет ограниченную вариацию), однако функция Gне имеет прямого вероятностного истолкования. Поэтому используют и другую форму представления Б. д. р., допускающую непосредственную вероятностную интерпретацию. Пусть функции Эти функции неубывающие, (каноническое представление Леви). Функции Важная роль Б. д. р. в предельных теоремах теории вероятностей связана с тем, что эти и только эти распределения могут быть предельными для сумм независимых случайных величин, подчиненных требованию асимптотической пренебрегаемости. При этом рассматривают последовательность серий
сходятся к предельному распределению (при нек-ром выборе констант Для симметричного распределения В других случаях выражение и только тогда, когда
Важным частным случаем Б. д. р. являются так наз. устойчивые распределения. См. также Безгранично делимых распределений разложение. Лит.:[1] Finetti В. de, "Atti Accad. naz. Lincei. Mem. Cl. sci. fis., mat. e natur, Sez. 1", ser. 6, 1929, v. 10, p. 163-68; [2] Колмогоров А. Н., там же, 1932, v. 15, p. 866-69; [3] Levу P., "Ann. Scuola Norm, di Pisa", 1934, v. 3, p. 337-66; [4] Levу Р., Theorie de 1'addition des variables aleatoires, P., 1937; [5] Xинчин А. Я., Предельные законы для сумм независимых случайных величин, М.-Л., 1938;[6] Гнеденко Б. В., Колмогоров А. Н., Предельные распределения для сумм независимых случайных величин, М.-Л., 1949; [7] Fisz M., "Ann. Math. Statist.", 1962, v. 33, p. 68-84; [8] Петров В. В., Суммы независимых случайных величин, М., 1972; [9] Сазонов В. В., Тутубалин В. Н., "Теория вероятн. и ее примен.", 1966, т. 11, с. 3-55. Ю. В. Прохоров. |
|
|
|

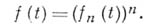
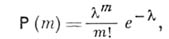
 не будет безгранично делимой, хотя ее распределение вероятностей (распределение Пуассона) есть Б. д. <р.
не будет безгранично делимой, хотя ее распределение вероятностей (распределение Пуассона) есть Б. д. <р.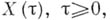 удовлетворяющие требованиям: 1)
удовлетворяющие требованиям: 1) 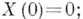 2) распределение вероятностей приращения
2) распределение вероятностей приращения 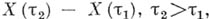 зависит только от
зависит только от 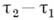 ; 3) при
; 3) при 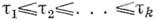 разности
разности 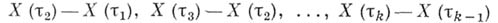
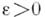
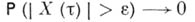
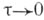 . Для такого процесса значение
. Для такого процесса значение 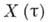 при любом
при любом 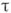 будет иметь Б. д. р. и соответствующая характеристич. функция удовлетворяет соотношению:
будет иметь Б. д. р. и соответствующая характеристич. функция удовлетворяет соотношению: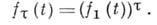
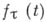 для таких процессов в предположении конечности дисперсий
для таких процессов в предположении конечности дисперсий 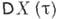 был найден А. Н. Колмогоровым [2] (частный случай приводимого ниже общего канонич. представления Б. д. р.).
был найден А. Н. Колмогоровым [2] (частный случай приводимого ниже общего канонич. представления Б. д. р.).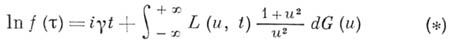
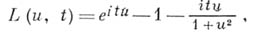
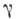 - нек-рая действительная постоянная,
- нек-рая действительная постоянная, 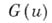 - неубывающая функция ограниченной вариации с
- неубывающая функция ограниченной вариации с 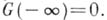 Подинтегральное выражение при
Подинтегральное выражение при 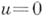 принимают равным
принимают равным 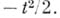 При любом выборе постоянной
При любом выборе постоянной 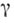 и функции
и функции 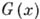 с указанными выше свойствами формула (*) определяет логарифм характеристич. функции нек-рого Б. д. р. Соответствие между Б. д. р. и парами
с указанными выше свойствами формула (*) определяет логарифм характеристич. функции нек-рого Б. д. р. Соответствие между Б. д. р. и парами 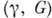 взаимно однозначно ивзаимно непрерывно. Последнее означает, что Б. д. р. слабо сходятся к предельному Б. д. р. тогда и только тогда, когда
взаимно однозначно ивзаимно непрерывно. Последнее означает, что Б. д. р. слабо сходятся к предельному Б. д. р. тогда и только тогда, когда 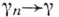 и
и 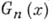 слабо сходятся к
слабо сходятся к 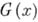 при
при 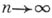 Примеры. Пусть
Примеры. Пусть 
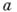 и дисперсией
и дисперсией 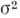 в формуле
в формуле 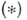 следует положить
следует положить 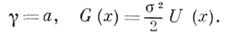
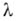 имеем
имеем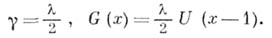
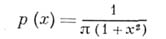
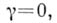
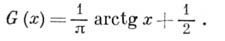
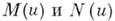 определены при
определены при 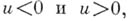 соответственно, формулами:
соответственно, формулами: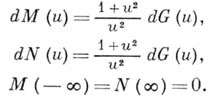
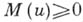 при
при 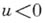 и
и 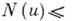
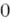 при
при 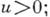 в окрестности нуля функции могут неограниченно возрастать. Обозначая дополнительно через s 2 скачок функции Gв нуле, формулу (*) можно переписать в виде:
в окрестности нуля функции могут неограниченно возрастать. Обозначая дополнительно через s 2 скачок функции Gв нуле, формулу (*) можно переписать в виде: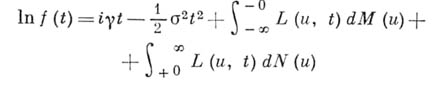
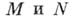 описывают, грубо говоря, частоту скачков различного размера в однородном процессе
описывают, грубо говоря, частоту скачков различного размера в однородном процессе 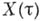 с независимыми приращениями, для к-рого
с независимыми приращениями, для к-рого 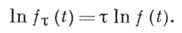
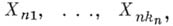
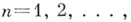 взаимно независимых случайных величин и затем подбирают взаимно независимые случайные величины
взаимно независимых случайных величин и затем подбирают взаимно независимые случайные величины 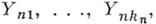 имеющие Б. д. р. (так наз. сопровождающие Б. д. р.); характеристич. функция
имеющие Б. д. р. (так наз. сопровождающие Б. д. р.); характеристич. функция 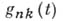 величины
величины 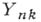 определяется по характеристич. функции
определяется по характеристич. функции 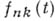 величины
величины 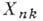 так, чтобы выполнялось следующее основное свойство: распределения сумм
так, чтобы выполнялось следующее основное свойство: распределения сумм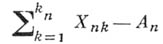
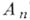 ) тогда и только тогда, когда сходятся к предельному распределения сумм
) тогда и только тогда, когда сходятся к предельному распределения сумм 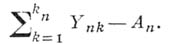
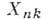 полагают
полагают 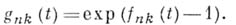
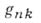 сложнее и содержит так наз. урезанные математич. ожидания
сложнее и содержит так наз. урезанные математич. ожидания 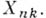 Свойства Б. д. р. описывают в терминах функций, входящих в канонич. представления. Так, напр., безгранично делимая функция распределения
Свойства Б. д. р. описывают в терминах функций, входящих в канонич. представления. Так, напр., безгранично делимая функция распределения 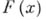 непрерывна тогда
непрерывна тогда