"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ОТРИЦАТЕЛЬНОЕ ПОЛИНОМИАЛЬНОЕ РАСПРЕДЕЛЕНИЕЗначение ОТРИЦАТЕЛЬНОЕ ПОЛИНОМИАЛЬНОЕ РАСПРЕДЕЛЕНИЕ в математической энциклопедии:
- совместное распределение вероятностей случайных величин  , принимающих неотрицательные целые значения m=0,1,2,..., заданное формулой , принимающих неотрицательные целые значения m=0,1,2,..., заданное формулой
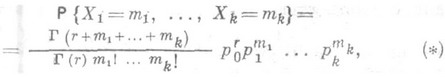
где r>0,  (0<р i<1, i=0,...,k; p0+...+pk=1) - параметры. О. п. р. является многомерным дискретным распределением - распределением случайного вектора (0<р i<1, i=0,...,k; p0+...+pk=1) - параметры. О. п. р. является многомерным дискретным распределением - распределением случайного вектора  с неотрицательными целочисленными компонентами. с неотрицательными целочисленными компонентами.
Производящая функция О. п. <р. с параметрами r,  имеет вид имеет вид
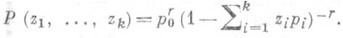
О. п. р. возникает в следующей полиномиальной схеме. Производятся последовательные независимые испытания, и в каждом испытании возможны k+1 различных исходов с индексами  к-рым соответствуют вероятности к-рым соответствуют вероятности 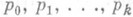 . Испытания продолжаются до r-го появления исхода с индексом О (здесь r - целое). Если Xi- число появлений исхода с индексом . Испытания продолжаются до r-го появления исхода с индексом О (здесь r - целое). Если Xi- число появлений исхода с индексом 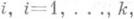 за время до конца испытаний, то формула (*) выражает вероятность появления исходов с индексами за время до конца испытаний, то формула (*) выражает вероятность появления исходов с индексами  соответственно, равно соответственно, равно  раз до r-го появления исхода 0. О. п. р. в указанном смысле служит обобщением отрицательного биномиального распределения, совпадая с последним при k=1. раз до r-го появления исхода 0. О. п. р. в указанном смысле служит обобщением отрицательного биномиального распределения, совпадая с последним при k=1.
Если случайный вектор 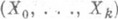 имеет полиномиальное распределение с параметрами n>1, р 0,..., pk и параметр псам является случайной величиной, имеющей отрицательное биномиальное распределение с параметрами имеет полиномиальное распределение с параметрами n>1, р 0,..., pk и параметр псам является случайной величиной, имеющей отрицательное биномиальное распределение с параметрами 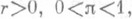 то распределение вектора то распределение вектора  при условии при условии 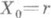 является О. п. р. с параметрами является О. п. р. с параметрами 
А. В. Прохоров.
|

 , принимающих неотрицательные целые значения m=0,1,2,..., заданное формулой
, принимающих неотрицательные целые значения m=0,1,2,..., заданное формулой 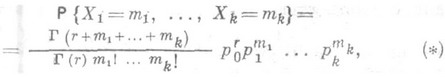
 (0<р i<1, i=0,...,k; p0+...+pk=1) - параметры. О. п. р. является многомерным дискретным распределением - распределением случайного вектора
(0<р i<1, i=0,...,k; p0+...+pk=1) - параметры. О. п. р. является многомерным дискретным распределением - распределением случайного вектора  с неотрицательными целочисленными компонентами.
с неотрицательными целочисленными компонентами. имеет вид
имеет вид 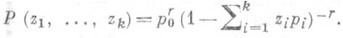
 к-рым соответствуют вероятности
к-рым соответствуют вероятности 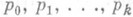 . Испытания продолжаются до r-го появления исхода с индексом О (здесь r - целое). Если Xi- число появлений исхода с индексом
. Испытания продолжаются до r-го появления исхода с индексом О (здесь r - целое). Если Xi- число появлений исхода с индексом 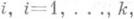 за время до конца испытаний, то формула (*) выражает вероятность появления исходов с индексами
за время до конца испытаний, то формула (*) выражает вероятность появления исходов с индексами  соответственно, равно
соответственно, равно  раз до r-го появления исхода 0. О. п. р. в указанном смысле служит обобщением отрицательного биномиального распределения, совпадая с последним при k=1.
раз до r-го появления исхода 0. О. п. р. в указанном смысле служит обобщением отрицательного биномиального распределения, совпадая с последним при k=1.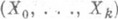 имеет полиномиальное распределение с параметрами n>1, р 0,..., pk и параметр псам является случайной величиной, имеющей отрицательное биномиальное распределение с параметрами
имеет полиномиальное распределение с параметрами n>1, р 0,..., pk и параметр псам является случайной величиной, имеющей отрицательное биномиальное распределение с параметрами 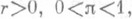 то распределение вектора
то распределение вектора  при условии
при условии 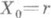 является О. п. р. с параметрами
является О. п. р. с параметрами 