|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ОТРИЦАТЕЛЬНОЕ БИНОМИАЛЬНОЕ РАСПРЕДЕЛЕНИЕЗначение ОТРИЦАТЕЛЬНОЕ БИНОМИАЛЬНОЕ РАСПРЕДЕЛЕНИЕ в математической энциклопедии: - распределение вероятностей случайной величины X, принимающей целые неотрицательные значения k = 0, 1, 2, ... в соответствии с формулой при любых действительных значениях параметров 0<р<1 и r>0. Производящая функция и характеристич. функция О. б. р. задаются формулами и где q=1- р. Математич. ожидание и дисперсия равны соответственно rq/p и rq/p2. Функция распределения О. б. р. для значений k=0,1,2,... определяется через значения функции бета-распределения в точке рследующим соотношением: где В (r, k + 1) - бета-функция. Происхождение термина "О. б. р." объясняется тем, что это распределение порождается биномом с отрицательным показателем, а именно, вероятности О. б. р. встречается во многих приложениях теории вероятностей. При целом r>0 О. б. р. интерпретируется как распределение времени ожидания г-го "успеха" в схеме Бернулли испытаний с вероятностью "успеха" р;в такой форме оно наз. обычно Паскаля распределением и является дискретным аналогом гамма-распределения. При r=1 О. б. р. совпадает с геометрическим распределением. Часто О. б. р. появляется в задачах, связанных с рандомизацией параметров распределений, напр, если Yслучайная величина, имеющая Пуассона распределение со случайным параметром l, к-рый в свою очередь имеет гамма-распределение с плотностью то распределение Yбудет О. б. р. с параметрами r=m и Сумма независимых случайных величин Х 1,...,Х n, имеющих О. б. р. с параметрами ри Лит.:[1] Ф е л л е р В., Введение в теорию вероятностей и ее приложения, пер. с англ., 2 изд., т. 1-2, М., 1967. А. В. Прохоров. |
|
|
|
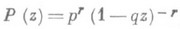
являются коэффициентами разложения 
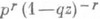по степеням z.
. О. б. р. служит предельной формой Пойа распределения.
соответственно, имеет О. б. р. с параметрами ри 
. При больших r и малых q, когда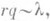 
О. б. р. приближается распределением Пуассона с параметром l. Многие свойства О. б. р. определяются тем фактом, что оно представляет собой обобщенное распределение Пуассона.