|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ОТНОШЕНИЕЗначение ОТНОШЕНИЕ в математической энциклопедии: - подмножество конечной декартовой степени Подмножество Одноместные О. наз. свойствами. Двуместные О. наз. бинарными, трехместные О. - тернарными и т. д. Множество А п ипустое подмножество наз. отношением равенства в множестве А. Если Rи Sсуть n-местные О. в множестве А, то га-местными О. в A будут также следующие подмножества в А n: Множество всех n-арных О. в множестве Аотносительно операций См. также Бинарное отношение. Соответствие. Д. М. Смирнов. |
|
|
|
данного множества А, т. е. подмножество систем (a1, а2,.., a п).из пэлементов множества А.
наз. п- местным, или n-арным, отношением в множестве А. Число n наз. рангом, или типом, отношения R. Подмножество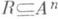 
наз. также n-местным, или n-арным, предикатом на множестве А . Запись 
означает, что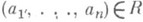 
.
в А" наз. соответственно универсальным отношением и нуль-отношением ранга пв множестве А. Диагональ множества А n, т. е. множество 
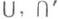является булевой алгеброй,(n+1 )-местное отношение Fв Аназ. функциональным, если для любых элементов 
из Аиз того, что 
, следует а=b.