"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ОТНОСИТЕЛЬНАЯ ГОМОЛОГИЧЕСКАЯ АЛГЕБРА
Значение ОТНОСИТЕЛЬНАЯ ГОМОЛОГИЧЕСКАЯ АЛГЕБРА в математической энциклопедии:
- гомологическая алгебра, ассоциированная с парой абелевых категорий 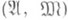 и фиксированным функтором
и фиксированным функтором  . Функтор
. Функтор  предполагается аддитивным, точным и полным. Короткая точная после довательность объектов категории
предполагается аддитивным, точным и полным. Короткая точная после довательность объектов категории 

наз. допустимой, если точная последовательность

расщепляется в категории  . Посредством класса
. Посредством класса  допустимых точных последовательностей определяется класс
допустимых точных последовательностей определяется класс  -проективных (соответственно
-проективных (соответственно  -инъективных) объектов как класс таких объектов Р(соответственно Q), для к-рых функтор
-инъективных) объектов как класс таких объектов Р(соответственно Q), для к-рых функтор  (соответственно
(соответственно  ) точен на допустимых коротких точных последовательностях.
) точен на допустимых коротких точных последовательностях.
Любом проективный объект Ркатегории  является
является  -проективным, это не означает, однако, что и категории
-проективным, это не означает, однако, что и категории  достаточно много относительно проективных объектов (т. е. что для любого объекта Аиз
достаточно много относительно проективных объектов (т. е. что для любого объекта Аиз  существует допустимый эпиморфизм
существует допустимый эпиморфизм  нск-рого
нск-рого
 - проективного объекта категории
- проективного объекта категории  ). Если в категории
). Если в категории  достаточно много
достаточно много  -проективных или
-проективных или
 - инъективных объектов, то обычные конструкции гомологлч. алгебры позволяют строить в этой категории производные функторы, наз. относительными производными функторами.
- инъективных объектов, то обычные конструкции гомологлч. алгебры позволяют строить в этой категории производные функторы, наз. относительными производными функторами.
П р и м е р ы. Пусть  - категория Д-модулей над ассоциативным кольцом R с единицей,
- категория Д-модулей над ассоциативным кольцом R с единицей,  - категория множеств,
- категория множеств,  - функтор, "забывающий" структуру модуля. В этом случае все точные последовательности допустимы, и в результате получается "абсолютная" (т. е. обычная) гомологич. алгебра.
- функтор, "забывающий" структуру модуля. В этом случае все точные последовательности допустимы, и в результате получается "абсолютная" (т. е. обычная) гомологич. алгебра.
Если G - группа, то каждый G-модуль является, в частности, абелевой группой. Если Нявляется алгеброй над коммутативным кольцом k, то каждый R-модуль, является k-модулем. Если Rи S - кольца и  , то каждый R-модуль является S-модулем. Во всех этих случаях имеется функтор из одной абелевой категории в другую, определяющий относительные производные функторы.
, то каждый R-модуль является S-модулем. Во всех этих случаях имеется функтор из одной абелевой категории в другую, определяющий относительные производные функторы.
Лит.:[1] Маклейн С., Гомология, пер. с англ., М., 1966; [2J EilenbergS., Moore J. С., Foundations of relative homological algebra, Providence, 1Я65.
В. Е. Говоров, А. В. Михалев.

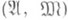 и фиксированным функтором
и фиксированным функтором  . Функтор
. Функтор  предполагается аддитивным, точным и полным. Короткая точная после довательность объектов категории
предполагается аддитивным, точным и полным. Короткая точная после довательность объектов категории 


 . Посредством класса
. Посредством класса  допустимых точных последовательностей определяется класс
допустимых точных последовательностей определяется класс  -проективных (соответственно
-проективных (соответственно  -инъективных) объектов как класс таких объектов Р(соответственно Q), для к-рых функтор
-инъективных) объектов как класс таких объектов Р(соответственно Q), для к-рых функтор  (соответственно
(соответственно  ) точен на допустимых коротких точных последовательностях.
) точен на допустимых коротких точных последовательностях. является
является  -проективным, это не означает, однако, что и категории
-проективным, это не означает, однако, что и категории  достаточно много относительно проективных объектов (т. е. что для любого объекта Аиз
достаточно много относительно проективных объектов (т. е. что для любого объекта Аиз  существует допустимый эпиморфизм
существует допустимый эпиморфизм  нск-рого
нск-рого  - проективного объекта категории
- проективного объекта категории  ). Если в категории
). Если в категории  достаточно много
достаточно много  -проективных или
-проективных или  - инъективных объектов, то обычные конструкции гомологлч. алгебры позволяют строить в этой категории производные функторы, наз. относительными производными функторами.
- инъективных объектов, то обычные конструкции гомологлч. алгебры позволяют строить в этой категории производные функторы, наз. относительными производными функторами. - категория Д-модулей над ассоциативным кольцом R с единицей,
- категория Д-модулей над ассоциативным кольцом R с единицей,  - категория множеств,
- категория множеств,  - функтор, "забывающий" структуру модуля. В этом случае все точные последовательности допустимы, и в результате получается "абсолютная" (т. е. обычная) гомологич. алгебра.
- функтор, "забывающий" структуру модуля. В этом случае все точные последовательности допустимы, и в результате получается "абсолютная" (т. е. обычная) гомологич. алгебра. , то каждый R-модуль является S-модулем. Во всех этих случаях имеется функтор из одной абелевой категории в другую, определяющий относительные производные функторы.
, то каждый R-модуль является S-модулем. Во всех этих случаях имеется функтор из одной абелевой категории в другую, определяющий относительные производные функторы.