|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
БАРЬЕРЗначение БАРЬЕР в математической энциклопедии: барьер Лебега, в теории потенциала- функция, существование к-рой является необходимым и достаточным условием регулярности граничной точки в отношении поведения обобщенного решения задачи Дирихле в этой точке (см. также Перрона метод. Регулярная точка). Пусть D - область в евклидовом пространстве где Б. в теории функций комплексного переменного- функция, из существования к-рой для всех граничных точек области Dследует, что Dявляется голоморфности областью. Пусть D - область в комплексном пространстве также существует Б. - функция Б. существует в граничной точке
Обратное справедливо для областей Лит.:[1] Курант Р., Уравнения с частными производными, пер. с англ., М., 1964, гл. 4; [2] Владимиров В. С., Методы теории функций многих комплексных переменных, М., 1964; [3] Шабат Б. В., Введение в комплексный анализ, ч. 2,2 изд., М., 1976. Е. Д. Соломенцев, М. Ширинбеков. |
|
|
|


 , и
, и  - точка ее границы
- точка ее границы  . Барьером для точки
. Барьером для точки  наз. всякая функция wx (x) , непрерывная в пересечении
наз. всякая функция wx (x) , непрерывная в пересечении  замкнутой области
замкнутой области  и нек-рого шара
и нек-рого шара  с центром в точке
с центром в точке  , супергармоническая внутри
, супергармоническая внутри  и положительная в
и положительная в  , за исключением точки
, за исключением точки  , в к-рой она обращается в нуль. Напр., при
, в к-рой она обращается в нуль. Напр., при  во всякой граничной точке
во всякой граничной точке  , для к-рой существует замкнутый шар
, для к-рой существует замкнутый шар  , имеющий с
, имеющий с  единственную общую точку
единственную общую точку  , в качестве Б. можно взять гармонич. функцию
, в качестве Б. можно взять гармонич. функцию 
 - радиус шара
- радиус шара  - его центр.
- его центр. - точка границы
- точка границы  . Б. в точке
. Б. в точке  есть всякая аналитич. функция
есть всякая аналитич. функция  , имеющая особенность в
, имеющая особенность в  . Так, для граничной точки
. Так, для граничной точки  любой плоской области
любой плоской области  Б. является функция
Б. является функция  . В каждой точке
. В каждой точке 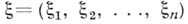 границы шара
границы шара 
 .
. области D, если в Dопределена аналитпч. функция
области D, если в Dопределена аналитпч. функция  , неограниченная в
, неограниченная в  , т. е. такая, что для нек-рой последовательности точек
, т. е. такая, что для нек-рой последовательности точек  , сходящейся к
, сходящейся к  , имеем
, имеем
 в следующей усиленной форме: для любого множества Еточек границы области D, в к-рых существует Б., найдется голоморфная в Dфункция, неограниченная во всех точках Е. Если Евсюду плотно на границе D, то D - область голоморфности.
в следующей усиленной форме: для любого множества Еточек границы области D, в к-рых существует Б., найдется голоморфная в Dфункция, неограниченная во всех точках Е. Если Евсюду плотно на границе D, то D - область голоморфности.