|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ОСТРОГРАДСКОГО МЕТОДЗначение ОСТРОГРАДСКОГО МЕТОД в математической энциклопедии: - метод выделения алгебраич. части у неопределенных интегралов от рациональных функции. Пусть Р(х).и Q(х).- многочлены с действительными коэффициентами, причем степень Р(х).меньше степени Q(х).и, следовательно, ai, pj, qj - действительные числа, Тогда существуют такие действительные многочлены Р 1 (х).п Р 2 (Х), степени к-рых меньше соответственно чем степени п 1 и n2=r+2s многочленов Q1(x).и Q2(x), что Важным является то обстоятельство, что многочлены Q1(x) н Q2(x).можно найти без знания разложения (1) многочлена Q(x).на неприводимые множители: многочлен Q1(x).является наибольшим общим делителем многочлена Q(х).и его производной Q' (х).и может быть получен с помощью алгоритма Евклида, a Q2(x)=Q(x)/Q1(x). Коэффициенты многочленов P1(x).и Р 2 (х).можно вычислить с помощью неопределенных коэффициентов метода. О. м. сводит, в частности, задачу интегрирования правильной рациональной дроби к задаче интегрирования правильной рациональной дроби, знаменатель к-рой имеет, простые корни; интеграл от такой функции выражается через трансцендентные функции: логарифмы и арктангенсы. Следовательно, рациональная дробь О. м. впервые опубликован М. В. Остроградским в 1845 (см. [1]). Лит.:[1] Остроградский М. <В. "Bull, scient. Acad. Sci. St.-Pitersbourg", 1845, t. 4,№ 10-11, p. 145-67; № 18-19, p. 280 - 300. Л. Д. Кудрявцев. |
|
|
|

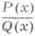 -правильная дробь,
-правильная дробь,
 и bi- - натуральные числа, i=l, 2, ..., r, j=1, 2, ..., s,
и bi- - натуральные числа, i=l, 2, ..., r, j=1, 2, ..., s,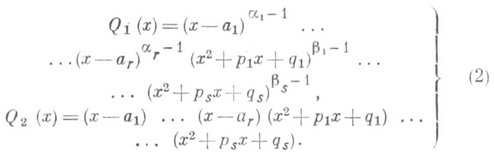

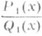 в формуле (3) является алгебраич. частью неопределенного интеграла
в формуле (3) является алгебраич. частью неопределенного интеграла 