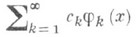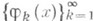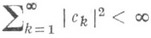|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ОРТОНОРМИРОВАННАЯ СИСТЕМАЗначение ОРТОНОРМИРОВАННАЯ СИСТЕМА в математической энциклопедии: - 1) О. с. векторов - множество М. И. Войцеховский. 2) О. с. ф у н к ц и и - система (см. Нормированная система, Ортогональная система). В математич. литературе часто термин "ортогональная система" означает "ортонормированная система". При исследовании данной ортогональной системы ее нормированность не играет существенной роли. Тем не менее нормированность систем дает возможность более ясной формулировки нек-рых теорем о сходимости рядов в терминах поведения коэффициентов по ортонормированной в L2[a, b]системе сходится в метрике пространства L2[a, b]тогда и только тогда, когда Лит.:[1] Колмогоров .А. Н., Фомин С. В., Элементы теории функций и функционального анализа, 5 изд., М., 1981; [2] Качмаж С., Штейнгауз Г., Теория ортогональных рядов, пер. с нем., М., 1958. А. А. Талалян. |
|
|
|

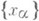 ненулевых векторов евклидова (гильбертова) пространства со скалярным произведением (. , .) такое, что
ненулевых векторов евклидова (гильбертова) пространства со скалярным произведением (. , .) такое, что 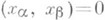 при
при 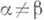 (ортогональность) и
(ортогональность) и 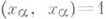 (нормируемость).
(нормируемость).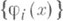 функций пространства L2(X, S,m,), являющаяся одновременно ортогональной и нормированной в L2(X, S,m), то есть
функций пространства L2(X, S,m,), являющаяся одновременно ортогональной и нормированной в L2(X, S,m), то есть 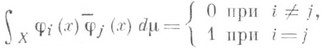
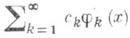
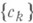 . Такой теоремой является, напр., теорема Рисса - Фигаера: ряд
. Такой теоремой является, напр., теорема Рисса - Фигаера: ряд