|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ОРТОМОДУЛЯРНАЯ РЕШЕТКАЗначение ОРТОМОДУЛЯРНАЯ РЕШЕТКА в математической энциклопедии: - решетка с нулем (0) и единицей (1), в к-рой для любого элемента асуществует ортодополнение и выполняется ортомодулярный закон: В О. р. исследовались в основном дистрибутивность н перспективность, неприводимость, модулярность пар. свойства центра и идеалов, коммутант и разрешимость, приложения к логике квантовой механики (см. [1], [2]). Если 1) 2) условие, двойственное к 1). Возникла задача построения абстрактной теории размерности в рамках такого класса решеток, к-рый включил бы в себя, кроме модулярных решеток проекций факторов типов In и II1 и немодулярные решетки проекций факторов остальных типов. Доказано (см. [5], [6]) существование функции размерности на полной О. р. с отношением эквивалентности, удовлетворяющим нек-рым дополнительным условиям. Этот класс решеток включает в себя и решетки проекций факторов, и непрерывные геометрии. О. р., являясь естественным обобщением решеток проекций факторов, в то же время составляют существенно более широкий класс, поскольку многие свойства решеток проекций неверны для произвольных О. р. Подобно тому как непрерывные геометрии координатизируются регулярными кольцами (см. [1]), О. р. могут быть координатизированы бэровскими Лит.:[1] Скорняков Л. А., Дедекиндовы структуры с дополнениями и регулярные кольца, М., 1961; [2] Итоги науки. Алгебра. Топология. Геометрия, 19(18, М., 1970; [3] Фофанова Т. С., в сб.: Упорядоченные множества и решетки, н. 3, [Саратов], 1975, с. 28 - 40; [4] Murray F., Neumann J., "Ann. Math.", 1936, v. 37, .№ l,p. 116-229;][5] L о о m i s L. H., "Mem. Amer. Math. Soc.", 1955, № 18, p. 1-36; [6] Маеda S., "J. Sci. Hiroshima Univ., Ser. A.", 1955, v. 19, № 2, p. 211 - 37; [7] Кap1anskу I., "Ann. Math.", 1955, v. 61, №3, p. 524- 541. Т. С. Фофанова. |
|
|
|

 , т. е. такой элемент, что
, т. е. такой элемент, что 

 - произвольная Неймана алгебра, то совокупность
- произвольная Неймана алгебра, то совокупность  всех ее проекций является полной О. р. При этом, если
всех ее проекций является полной О. р. При этом, если  - фактор, то на множестве
- фактор, то на множестве 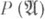 можно определить размерности, функцию. В зависимости от множества значений этой функции факторы делятся на типы
можно определить размерности, функцию. В зависимости от множества значений этой функции факторы делятся на типы  (классификация Муррея - Неймана, [4]). Было установлено, что решетки проекций факторов типа In и II1 являются непрерывными геометриями, т. <е. полными дедекиндовыми решетками с дополнениями, удовлетворяющими следующим двум аксиомам непрерывности:
(классификация Муррея - Неймана, [4]). Было установлено, что решетки проекций факторов типа In и II1 являются непрерывными геометриями, т. <е. полными дедекиндовыми решетками с дополнениями, удовлетворяющими следующим двум аксиомам непрерывности: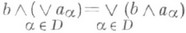 для любого направленного множества индексов Dи такого множества элементов
для любого направленного множества индексов Dи такого множества элементов 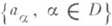 , что
, что  влечет
влечет  ;
; -полугруппами. Если полная О. р. модулярна, то она непрерывна (см. [7]). Существует модулярная решетка с ортодополнениями, пополнение сечениями к-рой не орто-модулярно (в то время как пополнение сечениями полумодулярной решетки с ортодополнениями полумодулярно, и решетка проекций алгебры Неймана полумодулярна).
-полугруппами. Если полная О. р. модулярна, то она непрерывна (см. [7]). Существует модулярная решетка с ортодополнениями, пополнение сечениями к-рой не орто-модулярно (в то время как пополнение сечениями полумодулярной решетки с ортодополнениями полумодулярно, и решетка проекций алгебры Неймана полумодулярна).