|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ОРТОГОНАЛЬНАЯ СИСТЕМАЗначение ОРТОГОНАЛЬНАЯ СИСТЕМА в математической энциклопедии: - 1) О. <с векто ров - множество {xa} ненулевых векторов евклидова (гильбертова) пространства со скалярным произведением 2) О. с. координат - система координат, и к-рой координатные линии (или поверхности) пересекаются под прямым углом. О. с. координат существуют в любом евклидовом пространстве, но, вообще говоря, не существуют в произвольном пространстве. В двумерном гладком аффинном пространстве О. с. всегда можно ввести по крайней мере в достаточно малой окрестности каждой точки. Иногда возможно введение О. с. координат в делом. В О. с. метрич. тензор gij диагоналей; диагональные компоненты gii принято наз. коэффициентами Ламе. Ламе коэффициент О. с. в пространстве выражаются формулами где x, у и z - декартовы прямоугольные координаты. Через коэффициенты Ламе выражаются элемент длины: элемент площади поверхности: элемент объема: векторные дифференциальные операции: Наиболее часто используемые О. с. координат: на плоскости - декартовы, полярные, эллиптические, параболические; в пространстве - сферические, цилиндрические, параболоидальные, бицилиндрические, биполярные. Д. Д. Соколов. 3) О. с. функций - конечная или счетная система {ji(x)} функций, принадлежащих пространству L2(X, S,m) и удовлетворяющих условиям Если li=1 для всех i, то система наз. ортонормированной. При этом предполагается, что мера m(x), определенная на s-алгебре Sподмножеств множества X, счетно аддитивна, полна и имеет счетную базу. Это определение О. с. включает все рассматриваемые в современном анализе О. с.; они получаются при различных конкретных реализациях пространства с мерой (X, S,m). Наибольший интерес представляют полные ортонормированные системы {jn(x)}, обладающие тем свойством, что для любой функции Такие системы существуют в силу сепарабельности пространства L2(X, S,m). Универсальный способ построения полных ортонормированных систем дает метод ортогонализации Шмидта. Для этого достаточно применить его к нек-рой полной L2(S, X,m) системе линейно независимых функций. В теории ортогональных рядов в основном рассматриваются О. с. пространЛва L2[a, b](тот частный случай, когда Х=[ а, b], S - система множеств, измеримых по Лебегу, и m - мера Лебега). Многие теоремы о сходимости или суммируемости рядов 1) Система Хаара где m=2n+k, 2) Система Радемахера представляет собой важный пример О. с. независимых функций и имеет применения как в теории вероятностей, так н в теории ортогональных и общих функциональных рядов. 3) Система Уолша - Пэли где числа ти qk определяются из двоичного разложения числа п: 4) Система Франклина Она является примером ортогонального базиса пространства С[0, 1] непрерывных функций. В теории кратных ортогональных рядов рассматриваются системы функций вида где Лит.:[l] Качмаж С., Штейнгауз Г., Теория ортогональных рядов, пер. с нем., М., 1958; [2] Итоги науки. Математический анализ, 1970, М., 1971, с. 109-46; [3] там же, с. 147- 202; [4] Дуб Д ж., Вероятностные процессы, пер. с англ., М., 1956; [5] Лоэв М., Теория вероятностей, пер. с англ., М., 1962; [6] Зигмунд А., Тригонометрические ряды, пер. с англ., т. 1-2, М., 1965. А. А. Талалян. |
|
|
|

 такое, что (xa, xab)=0 при
такое, что (xa, xab)=0 при  . Если при этом норма каждого вектора равна единице, то система {xa} наз. ортонормированной. Полная О. с. {xa} наз. ортогональным (ортонормированным) базисом. М. И. Войцеховский.
. Если при этом норма каждого вектора равна единице, то система {xa} наз. ортонормированной. Полная О. с. {xa} наз. ортогональным (ортонормированным) базисом. М. И. Войцеховский.

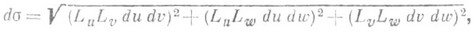



 существует единственный ряд
существует единственный ряд  , сходящийся к f(x) в метрике пространства L2(X, S,m), при этом коэффициенты с п определяются формулами Фурье
, сходящийся к f(x) в метрике пространства L2(X, S,m), при этом коэффициенты с п определяются формулами Фурье 
 ,
,  , по общим О. с. {jn(x)} пространства L2[a, b]верны и для рядов по ортонормированным системам пространства L2(X, S,m). Вместе с тем в этом частном случае построены интересные конкретные О. с., обладающие теми или иными хорошими свойствами. Таковы, например, системы Хаара, Радемахера, Уолша-Пэли, Франклина.
, по общим О. с. {jn(x)} пространства L2[a, b]верны и для рядов по ортонормированным системам пространства L2(X, S,m). Вместе с тем в этом частном случае построены интересные конкретные О. с., обладающие теми или иными хорошими свойствами. Таковы, например, системы Хаара, Радемахера, Уолша-Пэли, Франклина.


 , т=2,3, ... . Ряды по системе Хаара представляют типичный пример мартингалов и для них верны общие теоремы из теории мартингалов. Кроме того, система
, т=2,3, ... . Ряды по системе Хаара представляют типичный пример мартингалов и для них верны общие теоремы из теории мартингалов. Кроме того, система  является базисом в Lp[0,1],
является базисом в Lp[0,1],  , и ряд Фурье по системе Хаара любой интегрируемой функции почти всюду сходится.
, и ряд Фурье по системе Хаара любой интегрируемой функции почти всюду сходится.


 определяется через функции Радемахера:
определяется через функции Радемахера:

 получается ортогонализацией методом Шмидта последовательности функций
получается ортогонализацией методом Шмидта последовательности функций 

 - ортонормированная система в L2[a, b]. Такие системы ортонормированы на m-мерном кубе Jm =[a, b]x . ..x[ а, b] и полны, если полна система {jn(x)}
- ортонормированная система в L2[a, b]. Такие системы ортонормированы на m-мерном кубе Jm =[a, b]x . ..x[ а, b] и полны, если полна система {jn(x)}