ОПТИМАЛЬНОЕ ДЕКОДИРОВАНИЕ

Значение ОПТИМАЛЬНОЕ ДЕКОДИРОВАНИЕ в математической энциклопедии:

декодирование, к-рое максимизирует сообщений точность воспроизведения для заданных источников сообщений, канала связи и метода кодирования. В случае, когда точность воспроизведения сообщений характеризуется средней ошибочного декодирования вероятностью, О. д. минимизирует эту вероятность. Пусть, напр., для передачи Мсообщений, занумерованных числами 1,...,М, вероятности появления к-рых равны р ₁,...,р _M соответственно, используется дискретный канал с конечным числом значений сигналов на входе и выходе и переходной функцией, задаваемой матрицей

где Y, Y - множества значений сигналов h на входе и h^~ на выходе соответственно, а кодирование задается функцией такой, что f(m)=y_m,m=l,..., М, где 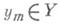, m=1,..., М,- код, т. е. нек-рый набор Мвозможных значений сигнала на входе канала. Тогда О. д. задается функцией такой, что для любого , где удовлетворяет неравенству

для всех . В частности, если все сообщения равновероятны, т. е. , то описанное О. д. является в то же время декодированием по методу "максимального правдоподобия" (к-рое в общем случае оптимальным не является): полученный на выходе канала сигнал следует декодировать в сообщение т', для к-рого

Лит.: [1] Галлагер Р., Теория информации и надежная связь, пер. с англ., М., 1974; [2] Возенкрафт Дж., Джекобе И., Теоретические основы техники связи, пер. с англ., М., 1969.Р. Л. Добрушип, В. В. Прелов.