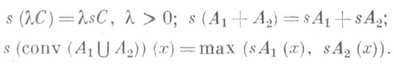|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ОПОРНАЯ ФУНКЦИЯЗначение ОПОРНАЯ ФУНКЦИЯ в математической энциклопедии: , опорный функционал, множества А, лежащего в векторном пространстве X, - функция sA, задаваемая в находящемся с ним в двойственности векторном пространстве Y соотношением Напр., О. ф. единичного тара в нормированном пространстве, рассматриваемом в двойственности со своим сопряженным пространством, - это норма в последнем. О. ф. всегда выпуклая, замкнутая и положительно однородная (первой степени). Оператор Примеры соотношений, связывающих оператор s с алгебраическими и теоретико-множественными операциями: Лит.:[1] Рокафеллар Р., Выпуклый анализ, пер. с англ., М., 1973; [2] Мinkоwski H., Geometric der Zalilen, Lpz,.-В., 1910; [3] его же, Gesammelte Abhandlungeri, Bd 2, Lpz.- В., 1911; [4] F e n с h e 1 W., "Canad. J. Malli.", 1949, v. I, p. 73-77; [5] e г о же, Convex cones, sets and funktions, Princeton, 1953; [6] Hогmander L., "Ark. for Mat.", 1955, bd 3, p. 181-86. В. М. Тихомиров. |
|
|
|


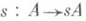 взаимно однозначно отображает совокупность выпуклых замкнутых множеств в Xна совокупность выпуклых замкнутых однородных функций, обратный оператор - не что иное, как субдифференциал (в нуле) опорной функции. Именно, если А - выпуклое замкнутое подмножество в X, то
взаимно однозначно отображает совокупность выпуклых замкнутых множеств в Xна совокупность выпуклых замкнутых однородных функций, обратный оператор - не что иное, как субдифференциал (в нуле) опорной функции. Именно, если А - выпуклое замкнутое подмножество в X, то  , и если р - выпуклая замкнутая однородная функция на Y, то
, и если р - выпуклая замкнутая однородная функция на Y, то  Эти два соотношения (являющиеся следствием теоремы Фенхеля - Моро, см. Сопряженная функция).и выражают двойственность между замкнутыми выпуклыми множествами и выпуклыми замкнутыми однородными функциями.
Эти два соотношения (являющиеся следствием теоремы Фенхеля - Моро, см. Сопряженная функция).и выражают двойственность между замкнутыми выпуклыми множествами и выпуклыми замкнутыми однородными функциями.