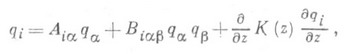ОКЕАНОЛОГИИ МАТЕМАТИЧЕСКИЕ ЗАДАЧИ

Значение ОКЕАНОЛОГИИ МАТЕМАТИЧЕСКИЕ ЗАДАЧИ в математической энциклопедии:

математические задачи в области физики, химии, геологии и биологии океана. В физике океана это прежде всего задачи геофизич. гидродинамики (определяемой как гидродинамика природных течений вращающихся бароклинных стратифицированных жидкостей). Вращение Земли, существенно влияющее на крупномасштабные течения (глобальных и синоптич. масштабов), и стратификация, т. е. изменение плотности среды по направлению силы тяжести (вертикали), создают специфич. анизотропию индивидуальных гидродинамич. полей в океане или их статистич. характеристик, к-рую необходимо учитывать, напр., при выборе базисных функций для описания этих полей по методу Галеркина, при объективном анализе (интерполяции, экстраполяции, сглаживании) эмпирич. данных об этих полях и выборе статистич. моделей для вертикально-неоднородных случайных полей турбулентности и внутренних волн.

Аналитич. описание собственных колебаний океана при помощи линеаризированных уравнений гидродинамики затрудняется из-за неправильной формы его границ - дна и берегов, что делает невозможным использование решений с разделяющимися неременными. Поэтому в теории приливов, в к-рой существенна возможность резонансных реакций океана на приливообразующие силы, имеются аналитич. расчеты лишь для модельных океанов правильной формы (напр., ограниченных отрезками меридианов и параллелей). В реальной же геометрии последовательные (возрастающие) собственные частоты должны определяться как экстремумы квадратичных интегральных функционалов, родственных энергии, на экстремалях, подбираемых по методу Галеркина; такой подход полностью еще не реализован. В теории приливов заметна не только линейная, но и нелинейная реакция океана на приливообразующие силы, к-рая может быть описана при представлении высоты прилива в виде функционального степенного ряда по приливообразующим силам; функциональные коэффициенты такого ряда описывают свойства океана как резонансной системы.

Для океана специфично наличие среди решений уравнений гидродинамики нескольких классов волн - акустических, поверхностных (капиллярных и гравитационных), внутренних гравитационных, инерционных (включая баротропные и бароклинные волны Росби - Блиновой, образующиеся вследствие изменения с широтой вертикальной проекции угловой скорости вращения Земли) и, наконец, гидромагнитных, возникающих при движениях электропроводной жидкости (соленой морской воды) в геомагнитном поле. Построение отдельных классов волновых решений (и динамич. уравнений для них) осуществляется при помощи асимптотич. методов нелинейной механики, родственных методу Ван дер Поля, в виде асимптотич. рядов по степеням малых параметров, стоящих при "лишних" производных по времени. Примером служит т. н. квазигеострофич. разложение, отфильтровывающее из числа решений уравнений гидродинамики быстрые волны и выделяющее класс волн Росби-Блиновой.

Волны в океане, как правило, нелинейны. Для длинных нелинейных волн, поверхностных и внутренних, удается вывести уравнение Кортевега-де Фриса н использовать его солитонные и периодические (кноидальные) решения. Для коротких волн сколько-нибудь общих методов нахождения солитонных и периодич. решений еще не построено, и существуют лишь отдельные примеры (капиллярные волны Слезкина - Краппера, гравитационные волны Герстнера и Стокса, баротропные и бароклинные солитоны Росби). Недостаточно развиты п статистич. теории нелинейных волновых полей, особенно актуальные для описания поверхностных и внутренних гравитационных волн (для внутренних волн - с генерацией ими турбулентных пятен и расплыванием последних в слои вертикальной микроструктуры) и волн Росби (с эволюцией квазидвумерной турбулентности в нелинейное волновое поле).

Одной из важнейших проблем гидродинамики океана является математич. моделирование его циркуляции (в наиболее общей постановке - в его взаимодействии с атмосферой через т. н. верхний перемешанный слой океана и пограничный слой атмосферы), причем вследствие большой ширины спектра масштабов пространственных неоднородностей (от миллиметров до 10⁴ километров) моделируемая система здесь имеет огромное число степеней свободы (при миллиметровых элементарных объемах порядка 10²⁸), и неизбежно возникает необходимость их аггрегирования, напр. методом параметризации мелкомасштабных процессов.

При аппроксимации континуальных гидродинамич. уравнений разностными возникают вопросы о порядке аппроксимации, сходимости и устойчивости разностной схемы. В современных т. н. вихреразрешающих моделях циркуляции океана используются пространственные сетки с горизонтальными шагами порядка немногих десятков километров. Конкурирующими могут быть схемы, использующие спектральные (в том числе галеркинские) разложения пространственных гидродинамич. полей.

Основные задачи математич. обработки данных измерений в гидродинамике океана делятся на задачи зондирования (функции от глубины, их разложения на моды, спектры), буксировки (горизонтальные и пространственно-временные спектры с доплеровскими эффектами) и полигонных измерений (временные ряды на трехмерной сетке точек, их спектры и взаимные спектры, объективный анализ, синхронные пространственные картины, четырехмерный анализ волновых полей).

В акустике океана рассматриваются типичные задачи распространения волн в слоистых средах; для аналитич. описания вертикальной структуры волновых полей в ряде случаев используется приближение ВКВ (см. ВКБ-метод). В оптике океана специфич. процессом является многократное рассеяние света, для описания к-рого используются численные решения уравнения переноса излучения, получаемые методами Монте-Карло, и асимптотические аналитич. решения. В химии океана важной математич. задачей является расчет конвективной диффузии неконсервативных примесей со специфич. источниками и стоками.

В геологии океана в связи с развитием мобилистской геотектоники (т. н. тектоники литосферных плит) возникли задачи кинематич. расчетов движения жестких плит на поверхности сферы и их генетич. объяснения при помощи математич. моделирования процессов плотностной конвекции в земной мантии (возникающей вследствие перехода тяжелых веществ из мантии в ядро). Одной из важных частных задач геологии является биостратиграфия, т. е. распознавание возрастов слоев осадочных пород по содержащимся в них микропалеонтологич. ассамблеям при помощи программ с самообучением (пока что в большинстве работ эта задача решается приближенно без использования ЭВМ).

Весьма объемные вычислительные задачи оценки ста-тистич. характеристик сигналов, фильтрации шумов и распознавания образов возникают при регистрации и обработке данных морского многоканального непрерывного глубинного сейсмопрофилирования и вибропросвечивания океанского дна, причем в ряде случаев и при постановке измерений (пространственные распределения излучателей и приемников сигналов), и при их регистрации перспективны голографич. методы, использующие преобразования Фурье.

В биологии океана в проблеме управления биология, продуктивностью океана важное значение приобретает математич. моделирование структуры и функционирования экологич. систем и, в частности, динамики популяций. Примером служит аадача об эволюции со временем tвертикальных распределений g_i (z, t) компонент q_i экологич. системы (включающих концентрации ряда видов фито- и зоопланктона, кислорода, углекислого газа, фосфорных и азотных солей, температуру и соленость воды, освещенность фотосинтетически-активной радиацией), описываемой уравнениями вида

где A_ia, B_ia_B- биологич. и биофизич. параметры; здесь представляют интерес как численные решения задачи Коши с конкретными начальными данными, так и выводы качественной теории дифференциальных уравнений о поведении решений в целом и об их зависимости от имеющихся в уравнениях параметров.

Лит.:[1] Биология океана, т. 1-2, М., 1977; [2] Физика океана, т. 1, М., 1978; [3] Геофизика океана, т. 1-2, М., 1979; [4] Химия океана, т. 1-2, М., 1979; [5] Геология океана, т. 1, М., 1979. А. С. Монин.