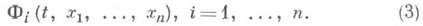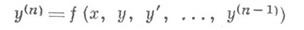|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ОБЩИЙ ИНТЕГРАЛЗначение ОБЩИЙ ИНТЕГРАЛ в математической энциклопедии: системы обыкновенных дифференциальных уравнений n -го порядка
в области G- совокупность псоотношений
содержащая ппараметров
Каждое из соотношений (2) [или каждая из функций (3)] наз. первым интегралом системы (1). Иногда под О. и. системы (1) понимают совокупность более общих, чем (2), соотношений
В случае обыкновенного дифференциального уравнения п-го порядка
О. и. в области Gпредставляет собой одно соотношение с ппараметрами
в виде неявной функции описывающее общее решение этого уравнения в области G. О. и. дифференциального уравнения с частными производными 1-го порядка наз. соотношение между входящими в уравнение переменными, содержащее одну произвольную функцию и определяющее при каждом выборе этой функции решение уравнения. См. также Интеграл дифференциального уравнения. Лит. см. при ст. Общее решение. Н. X. Ролов. |
|
|
|


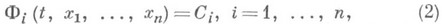
 и в неявном виде описывающая семейство функций, составляющих
и в неявном виде описывающая семейство функций, составляющих