"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
БАЗИС
Значение БАЗИС в математической энциклопедии:
множества X - минимальное порождающее его подмножество В. Порождение означает, что применением операций нек-рого класса  к элементам
к элементам  получается любой элемент
получается любой элемент  Это понятие связано с понятием зависимости: элементы Xпосредством операций из
Это понятие связано с понятием зависимости: элементы Xпосредством операций из  ставятся в зависимость от элементов В. Минимальность означает, что никакое собственное подмножество
ставятся в зависимость от элементов В. Минимальность означает, что никакое собственное подмножество  не порождает X. Это свойство обусловливает в нек-ром смысле независимость его элементов: никакой элемент
не порождает X. Это свойство обусловливает в нек-ром смысле независимость его элементов: никакой элемент  не порождается остальными его элементами. Напр., множество всех натуральных чисел
не порождается остальными его элементами. Напр., множество всех натуральных чисел  имеет Б. единствевг-ный элемент 0 и порождается из него операцией непосредственного следования и ее итерациями; множество всех натуральных чисел
имеет Б. единствевг-ный элемент 0 и порождается из него операцией непосредственного следования и ее итерациями; множество всех натуральных чисел  порождается операцией умножения из Б., состоящего из всех простых чисел. Базис алгебры кватернионов состоит из четырех элементов
порождается операцией умножения из Б., состоящего из всех простых чисел. Базис алгебры кватернионов состоит из четырех элементов  если порождающими операциями являются сложение и умножение на действительные числа; если же кроме этих операций используется еще и умножение кватернионов, то Б. будет состоять лишь из трех элементов
если порождающими операциями являются сложение и умножение на действительные числа; если же кроме этих операций используется еще и умножение кватернионов, то Б. будет состоять лишь из трех элементов  (ибо
(ибо  ).
).
Базис натурального ряда порядка  - подпоследовательность
- подпоследовательность  множества
множества  натуральных чисел с включением 0, к-рая в результате Декретного сложения с собой (операция порождения) дает все
натуральных чисел с включением 0, к-рая в результате Декретного сложения с собой (операция порождения) дает все  Это означает, что каждое натуральное число ппредставимо в виде
Это означает, что каждое натуральное число ппредставимо в виде

где  Напр., всякое натуральное число есть сумма четырех квадратов натуральных чисел (теорема Лагранжа), т. е. последовательность квадратов есть Б.
Напр., всякое натуральное число есть сумма четырех квадратов натуральных чисел (теорема Лагранжа), т. е. последовательность квадратов есть Б.  порядка 4. Вообще, последовательность
порядка 4. Вообще, последовательность  степеней натуральных чисел является Б.
степеней натуральных чисел является Б.  (теорема Гильберта), порядок к-рого оценивается Виноградова методом. Понятие Б.
(теорема Гильберта), порядок к-рого оценивается Виноградова методом. Понятие Б.  обобщается на случай произвольных числовых последовательностей, т. е. функций на
обобщается на случай произвольных числовых последовательностей, т. е. функций на  .
.
Порождающие  множества существуют всегда (тривиально:
множества существуют всегда (тривиально:  порождает
порождает  ), однако минимальность может оказаться принципиально невозможной (подобная ситуация типична для классов
), однако минимальность может оказаться принципиально невозможной (подобная ситуация типична для классов  , содержащих бес-конечноместные операции, в частности в топологич. структурах, решетках и т. п.). Поэтому условие минимальности заменяется более слабым требованием: Б. есть порождающее множество минимальной мощности. В связи с этим обычно
, содержащих бес-конечноместные операции, в частности в топологич. структурах, решетках и т. п.). Поэтому условие минимальности заменяется более слабым требованием: Б. есть порождающее множество минимальной мощности. В связи с этим обычно  . Вопределяется как параметризованное множество (или семейство), т. е. как функция
. Вопределяется как параметризованное множество (или семейство), т. е. как функция  на множестве индексов
на множестве индексов  со значениями в
со значениями в  , причем
, причем  ; мощность Тиногда наз. базисной размерностью (или рангом)
; мощность Тиногда наз. базисной размерностью (или рангом) Напр., счетное всюду плотное множество
Напр., счетное всюду плотное множество  сепарабель-ного топологич. пространства
сепарабель-ного топологич. пространства  можно считать его
можно считать его  .;
.;  порождается из
порождается из  операцией замыкания (к-рая, кстати, и в более общих случаях родственна порождению, см. ниже).
операцией замыкания (к-рая, кстати, и в более общих случаях родственна порождению, см. ниже).
Базис топологии топологич. пространства
 (база) - Б.
(база) - Б.  совокупности всех открытых подмножеств X;порождение осуществляется объединением элементов
совокупности всех открытых подмножеств X;порождение осуществляется объединением элементов 
Базис булевой алгебры  (двойственный базе
(двойственный базе  в смысле Тарского) - плотное множество (минимальной мощности)
в смысле Тарского) - плотное множество (минимальной мощности)  в
в  ; порождение
; порождение  из
из  (а тем самым и само
(а тем самым и само  ) определяется условием
) определяется условием  (что равносильно
(что равносильно  ), где
), где  ,
,  ,
,  - единица
- единица  ,
,  - операция импликации. Аналогично вводится ибазис фильтра
- операция импликации. Аналогично вводится ибазис фильтра  , как множество
, как множество  такое, что для любого
такое, что для любого  существует
существует  , и
, и  .
.
Большинство частных случаев Б. множества  вводится по следующей схеме. Пусть
вводится по следующей схеме. Пусть 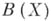 - булеан
- булеан  , т. е. совокупность всех его подмножеств. Порождающим оператором (или оператором замыкания)
, т. е. совокупность всех его подмножеств. Порождающим оператором (или оператором замыкания)  называется отображение
называется отображение  в себя такое, что: если
в себя такое, что: если 

Элемент  порождается множеством
порождается множеством  , если
, если  в частности,
в частности, порождает
порождает  , если
, если 
 . Минимальное множество
. Минимальное множество  , обладающее этим свойством, и наз. базисом
, обладающее этим свойством, и наз. базисом  .определенным оператором
.определенным оператором  . Порождающий оператор J имеет конечный тип, если для любых
. Порождающий оператор J имеет конечный тип, если для любых  из
из  следует
следует  для нек-рого конечного подмножества
для нек-рого конечного подмножества  порождающий оператор
порождающий оператор  обладает свойством замещения, если для любых
обладает свойством замещения, если для любых  следует
следует  Порождающий оператор
Порождающий оператор  конечного типа со свойством замещения определяет на X отношение зависимости, т. е. разбиение
конечного типа со свойством замещения определяет на X отношение зависимости, т. е. разбиение  на два класса - зависимых и независимых множеств; множество Аназ. зависимым, если
на два класса - зависимых и независимых множеств; множество Аназ. зависимым, если  для нек-рого
для нек-рого  , и независимым, если
, и независимым, если  для любого
для любого  . При этом
. При этом  зависимо (независимо) тогда и только тогда, когда некоторое (любое) непустое конечное подмножество
зависимо (независимо) тогда и только тогда, когда некоторое (любое) непустое конечное подмножество  зависимо (независимо).
зависимо (независимо).
Для того чтобы множество  было Б. множества
было Б. множества  , необходимо н достаточно, чтобы
, необходимо н достаточно, чтобы  было независимым порождающим
было независимым порождающим  множеством или, иначе, максимальным независимым в
множеством или, иначе, максимальным независимым в  множеством.
множеством.
Если  - произвольное независимое множество, а С - порождающее
- произвольное независимое множество, а С - порождающее  множество, содержащее А, то существует Б. Вв X такой, что
множество, содержащее А, то существует Б. Вв X такой, что  В частности, Xвсегда обладает Б., и любые два его Б. равно-мощны.
В частности, Xвсегда обладает Б., и любые два его Б. равно-мощны.
В алгебраич. системах X важную роль играет понятие так наз. свободного базиса В, характеризующегося следующим свойством: произвольное отображение  в любую алгебраич. систему
в любую алгебраич. систему  (той же сигнатуры) может быть продолжено до (гомо) морфизма
(той же сигнатуры) может быть продолжено до (гомо) морфизма  в
в  , пли, что то же самое, для любого (гомо)морфизма
, пли, что то же самое, для любого (гомо)морфизма  и любого множества
и любого множества  порождающие операторы
порождающие операторы  удовлетворяют условию:
удовлетворяют условию:

Алгебрапч. система, имеющая свободный В., наз. свободной.
Типичным примером является базис (унитарного) модуля Mнад кольцом К - свободное семейство элементов из М, порождающее М(см. [3]). Здесь семейство  элементов K-модуля Мназ. свободным, если из
элементов K-модуля Мназ. свободным, если из  (где
(где  для всех, кроме конечного числа индексов
для всех, кроме конечного числа индексов  следует
следует  для всех
для всех  , а порождение осуществляется представлением элементов хв виде линейных комбинаций элементов
, а порождение осуществляется представлением элементов хв виде линейных комбинаций элементов  : существует (зависящее от х).множество элементов
: существует (зависящее от х).множество элементов  такое, что
такое, что  для всех, кроме конечного числа индексов t, и имеет место разложение
для всех, кроме конечного числа индексов t, и имеет место разложение

(т. е. X- линейная оболочка A). Б. Мв этом смысле является его свободным Б. в вышеуказанном смысле; обратное также верно. Так, множество периодов двоякопериодич. функции  одного комплексного переменного, являющееся дискретной абелевой группой (и потому модулем над кольцом
одного комплексного переменного, являющееся дискретной абелевой группой (и потому модулем над кольцом  ). имеет свободный Б., наз. базисом периодов функции
). имеет свободный Б., наз. базисом периодов функции  ; он состоит из двух так наз. примитивных периодов. Аналогично определяется Б. периодов абелевой функции нескольких комплексных переменных.
; он состоит из двух так наз. примитивных периодов. Аналогично определяется Б. периодов абелевой функции нескольких комплексных переменных.
В случае, когда К - тело, всякий Б. (в прежнемсмысле) является свободным. Напротив, существуют модули, не имеющие свободного Б.; таковы, напр., неглавные идеалы в области целостности К, рассматриваемой как K-модуль.
Базис векторного пространства X над полем К- (свободный) В. подлежащего Xунитарного модуля. Аналогично, базис алгебры Анад полем К - Б. подлежащего A векторного пространства. Все Б. данного векторного пространства Xимеют одинаковую мощность, равную мощности Т, к-рая наз. его алгебраической размерностью. Каждый элемент  представим линейной комбинацией элементов Б. единственным образом. Элементы
представим линейной комбинацией элементов Б. единственным образом. Элементы  , являющиеся линейными функционалами на X, наз. компонентами (координатами)
, являющиеся линейными функционалами на X, наз. компонентами (координатами)  в данном Б.
в данном Б. .
.
Множество Аявляется Б. в Xтогда и только тогда, когда А - максимальное (относительно включения) свободное множество в X.
Отображение

где  , если
, если  - значение t-й компоненты хв Б. A и 0 в противном случае, наз. базисным отображением; оно является линейным инъективным отображением Xв пространство
- значение t-й компоненты хв Б. A и 0 в противном случае, наз. базисным отображением; оно является линейным инъективным отображением Xв пространство  функций на Тсо значениями в K. В данном случае образ
функций на Тсо значениями в K. В данном случае образ  состоит из функций с конечным числом значений, отличных от нуля (конечнозначных функций). Эта интерпретация позволяет определить обобщенный базис векторного пространства
состоит из функций с конечным числом значений, отличных от нуля (конечнозначных функций). Эта интерпретация позволяет определить обобщенный базис векторного пространства  над полем
над полем  как биективное линейное отображение его на нек-рое подпространство
как биективное линейное отображение его на нек-рое подпространство  пространства
пространства  функций на
функций на  со значениями в
со значениями в  , где
, где  - нек-рое надлежащим образом подобранное множество. Однако без введения дополнительных ограничений на
- нек-рое надлежащим образом подобранное множество. Однако без введения дополнительных ограничений на  (напр., порядка) и структур на
(напр., порядка) и структур на  (напр., топологии) и согласованных с этим условий на
(напр., топологии) и согласованных с этим условий на  понятие обобщенного Б. практически мало полезно.
понятие обобщенного Б. практически мало полезно.
Иногда Б. векторного пространства  наз. алгебраическим базисом (чем подчеркивается отсутствие связи с дополнительными структурами на
наз. алгебраическим базисом (чем подчеркивается отсутствие связи с дополнительными структурами на  , даже если они и согласованы с его векторной структурой).
, даже если они и согласованы с его векторной структурой).
Базис Гамеля (Хамеля) - Б. поля действительных чисел R, рассматриваемого как векторное пространство над полем рациональных чисел. Введен Г. Гамелем [4] для получения разрывного решения функционального уравнения  ; график решения его всюду плотен на плоскости
; график решения его всюду плотен на плоскости  . Каждой почти периодич. функции
. Каждой почти периодич. функции  соответствует нек-рый счетный базис Гамеля
соответствует нек-рый счетный базис Гамеля  такой, что каждый показатель Фурье
такой, что каждый показатель Фурье  этой функции принадлежит линейной оболочке
этой функции принадлежит линейной оболочке  . При этом элементы
. При этом элементы  можно выбрать принадлежащими последовательности
можно выбрать принадлежащими последовательности  ; множество
; множество  наз. базисом почтп периодической функции. Аналогичный Б. строится в кольце, содержащем тело Ри имеющем единицу тела Рсвоей единицей. Алгебраич. Б. произвольного векторного пространства также наз. иногда базисом Гамеля.
наз. базисом почтп периодической функции. Аналогичный Б. строится в кольце, содержащем тело Ри имеющем единицу тела Рсвоей единицей. Алгебраич. Б. произвольного векторного пространства также наз. иногда базисом Гамеля.
Базис топологический (Б. топологического векторного пространства Xнад полем К) - семейство  , свойства и функции к-рого аналогичны свойствам н функциям алгебраич. Б. векторного пространства. Понятие топологич. В.- одно из важнейших в функциональном анализе - расширяет и углубляет понятие алгебраич. Б. с учетом топологич. структуры X и позволяет получать для каждого элемента
, свойства и функции к-рого аналогичны свойствам н функциям алгебраич. Б. векторного пространства. Понятие топологич. В.- одно из важнейших в функциональном анализе - расширяет и углубляет понятие алгебраич. Б. с учетом топологич. структуры X и позволяет получать для каждого элемента  его разложение по Б.
его разложение по Б.  и притом единственное, т. е. представление хв виде предела (в том или ином смысле) линейных комбинаций элементов
и притом единственное, т. е. представление хв виде предела (в том или ином смысле) линейных комбинаций элементов  :
: где
где  - линейные функционалы на Xсо значениями в К, наз. компонентами х в Б . А, или коэффициентами разложениям по Б. А. Очевидно, для существования разложения любого хнеобходимо, чтобы Абыло полным множеством в X, а для единственности такого разложения (т. е. для того, чтобы нулевой элемент Xимел все компоненты равными нулю) необходимо, чтобы Абыло топологическим свободным множеством в X.
- линейные функционалы на Xсо значениями в К, наз. компонентами х в Б . А, или коэффициентами разложениям по Б. А. Очевидно, для существования разложения любого хнеобходимо, чтобы Абыло полным множеством в X, а для единственности такого разложения (т. е. для того, чтобы нулевой элемент Xимел все компоненты равными нулю) необходимо, чтобы Абыло топологическим свободным множеством в X.
Смысл и практич. значение топологич. Б. (наз. далее просто Б.) заключается в установлении биективного линейного отображения X, наз. базисным отображением  , на нек-рое, зависящее от X, пространство
, на нек-рое, зависящее от X, пространство  функций со значениями в К, определенных на (топологическом) пространстве Т, а именно:
функций со значениями в К, определенных на (топологическом) пространстве Т, а именно:

где  , так что символически
, так что символически  и
и  ; при этом строение
; при этом строение  вследствие конкретности, эффективности своего определения проще и обозримее, чем строение абстрактно заданного
вследствие конкретности, эффективности своего определения проще и обозримее, чем строение абстрактно заданного  . Так, напр., алгебраич. Б. бесконечномерного банахова пространства несчетен, в то время как в ряде случаев при надлежащем обобщении понятия Б. мощность
. Так, напр., алгебраич. Б. бесконечномерного банахова пространства несчетен, в то время как в ряде случаев при надлежащем обобщении понятия Б. мощность  существенно уменьшается, одновременно упрощается и
существенно уменьшается, одновременно упрощается и  .
.
Пространство  содержит все конечнозначные функции, и множество элементов Б.
содержит все конечнозначные функции, и множество элементов Б.  является биективным прообразом множества функций
является биективным прообразом множества функций  , имеющих лишь одно ненулевое значение, равное 1 ("однозначных" функций):
, имеющих лишь одно ненулевое значение, равное 1 ("однозначных" функций): где
где  при
при  . Другими словами,
. Другими словами, - образующая одномерного подпространства
- образующая одномерного подпространства  , дополнительного в Xк гиперплоскости, определяемой уравнением
, дополнительного в Xк гиперплоскости, определяемой уравнением 
Таким образом, роль Б.  сводится к организации из множества компонент
сводится к организации из множества компонент  , составляющих образ хпри базисном отображении, суммируемого (в том или ином смысле) семейства
, составляющих образ хпри базисном отображении, суммируемого (в том или ином смысле) семейства  , т. е. Б. "разлагает" пространство Xв (обобщенную) прямую сумму одномерных подпространств:
, т. е. Б. "разлагает" пространство Xв (обобщенную) прямую сумму одномерных подпространств:

Аналогичным образом определяется Б. в векторных пространствах, наделенных равномерной, предельной (псевдотопологической), линейной  , близостной и другими дополнительными структурами.
, близостной и другими дополнительными структурами.
Мыслимы (и существуют) обобщения понятия Б., идущие в различных направлениях. Так, введение топологии и меры на Тприводит к понятию так наз. непрерывной суммы элементов из Xи соответствующим интегральным представлениям; разложение пространства Xна необязательно одномерные компоненты находит применение в спектральной теории линейных операторов; рассмотрение вместо К(Т).произвольных топологич. алгебр над полем К(напр., алгебры мер на Тсо значениями в Кили даже в X, алгебры проекторов и т. д.) позволяет конкретизировать многие понятия абстрактной двойственности для топологич. векторных пространств и, в частности, использовать развитый аппарат теории характеров.
Базис счетный- наиболее исследованный (и в то же время практически наиболее важный) пример Б.- последовательность  элементов пространства Xтакая, что каждому элементу ходнозначно соответствует разложение его в ряд по Б.
элементов пространства Xтакая, что каждому элементу ходнозначно соответствует разложение его в ряд по Б.

сходящийся (в топологии X).к х. Здесь  причем существен естественный порядок в нем. Часто счетный Б. наз. просто Б. [Аналогично, если подразумевается слабая сходимость разложения х, определяется слабый счетный базис.] Так, напр., функции
причем существен естественный порядок в нем. Часто счетный Б. наз. просто Б. [Аналогично, если подразумевается слабая сходимость разложения х, определяется слабый счетный базис.] Так, напр., функции  ,
,  образуют Б. в пространствах
образуют Б. в пространствах  (абсолютно суммируемых в степени рпериодич. функций), напротив, в пространствах
(абсолютно суммируемых в степени рпериодич. функций), напротив, в пространствах  (измеримых функций, совпадающих почти всюду с ограниченными функциями) и
(измеримых функций, совпадающих почти всюду с ограниченными функциями) и  (непрерывных периодич. функций) эти функции Б. не образуют. Необходимым (но далеко не достаточным) условием существования счетного Б. является сепарабельность
(непрерывных периодич. функций) эти функции Б. не образуют. Необходимым (но далеко не достаточным) условием существования счетного Б. является сепарабельность  (напр., в пространстве измеримых на отрезке
(напр., в пространстве измеримых на отрезке  функций со значениями в
функций со значениями в  счетного Б. быть не может). Впрочем, пространство
счетного Б. быть не может). Впрочем, пространство  ограниченных последовательностей, не будучи сепарабельным в топологии
ограниченных последовательностей, не будучи сепарабельным в топологии  , не обладает счетным Б., однако элементы
, не обладает счетным Б., однако элементы 
 , где
, где  при
при  и
и  при
при  , образуют Б. в слабой топологии
, образуют Б. в слабой топологии  . Вопрос о существовании счетного Б. в сепарабельных банаховых пространствах (проблема базиса) решен отрицательно [6]. Аналогичный вопрос для ядерных пространств также решен отрицательно [7].
. Вопрос о существовании счетного Б. в сепарабельных банаховых пространствах (проблема базиса) решен отрицательно [6]. Аналогичный вопрос для ядерных пространств также решен отрицательно [7].
Счетный Б., однако, не всегда оказывается "достаточно хорошим" для применений (напр., компоненты  не являются непрерывными, разложение
не являются непрерывными, разложение  не сходится безусловно и т. п.), в связи с чем на Б. накладываются некоторые условия или вводится надлежащее его обобщение.
не сходится безусловно и т. п.), в связи с чем на Б. накладываются некоторые условия или вводится надлежащее его обобщение.
Базис счетного типа - одно из обобщений понятия счетного В., для к-рого хотя  и несчетно, но разложение элемента
и несчетно, но разложение элемента  по нему естественно определяется: соответствующее пространство
по нему естественно определяется: соответствующее пространство  состоит из счетнозначных функций. Напр., полное орто-нормированное множество
состоит из счетнозначных функций. Напр., полное орто-нормированное множество  в гильбертовом пространстве Нявляется Б.; если
в гильбертовом пространстве Нявляется Б.; если  , то
, то  (где
(где  - скалярное произведение в Н).для всех, за исключением быть может счетного множества, индексов
- скалярное произведение в Н).для всех, за исключением быть может счетного множества, индексов  , и ряд
, и ряд  сходится к х. Базисное отображение определяется ортогональным проектированием на замкнутые подпространства, порожденные элементами
сходится к х. Базисное отображение определяется ортогональным проектированием на замкнутые подпространства, порожденные элементами  Б. пространства
Б. пространства  всех комплекснозначных почти периодич. функций на
всех комплекснозначных почти периодич. функций на  состоит из функций
состоит из функций  ; здесь
; здесь  - совокупность счетнозначных функций, а базисное отображение определяется формулой
- совокупность счетнозначных функций, а базисное отображение определяется формулой

Базис безусловный- счетный Б. в пространстве Xтакой, что разложение любого элемента хсходится безусловно (т. <е. сумма ряда не изменяется при перестановке любого числа его слагаемых). Так, напр., в пространствах  (последовательностей, сходящихся к нулю) и
(последовательностей, сходящихся к нулю) и  (последовательностей, суммирую мых в степени
(последовательностей, суммирую мых в степени  ) элементы
) элементы  образуют безусловный Б.; в пространстве
образуют безусловный Б.; в пространстве  непрерывных на отрезке
непрерывных на отрезке  функций (любой) Б. не может быть безусловным. Ортонормированный счетный Б. гильбертова пространства - безусловный Б. Банахово пространство с безусловным Б. слабо полно (соответственно обладает сепарабельным сопряженным пространством) в том и только в том случае, когда оно не содержит подпространства, изоморфного с 0 (соответственно
функций (любой) Б. не может быть безусловным. Ортонормированный счетный Б. гильбертова пространства - безусловный Б. Банахово пространство с безусловным Б. слабо полно (соответственно обладает сепарабельным сопряженным пространством) в том и только в том случае, когда оно не содержит подпространства, изоморфного с 0 (соответственно  ).
).
Б.  и
и  соответствующих банаховых пространств Xи Yназ. эквивалентными, если существует биективное линейное отображение Т:
соответствующих банаховых пространств Xи Yназ. эквивалентными, если существует биективное линейное отображение Т: , распространяемое до изоморфизма Xв Y;эти Б. наз. квазиэквивалентными, если они становятся эквивалентными после нек-рой перестановки и нормировки элементов одного из них. Пространства
, распространяемое до изоморфизма Xв Y;эти Б. наз. квазиэквивалентными, если они становятся эквивалентными после нек-рой перестановки и нормировки элементов одного из них. Пространства  обладают тем свойством, что в каждом из них все нормированные безусловные Б. эквивалентны. В декартовом произведении
обладают тем свойством, что в каждом из них все нормированные безусловные Б. эквивалентны. В декартовом произведении  квазиэквивалентны все безусловные Б. Существуют, однако, нормированные Б., не эквивалентные ортонормированному.
квазиэквивалентны все безусловные Б. Существуют, однако, нормированные Б., не эквивалентные ортонормированному.
Базис суммирующий - обобщение понятия безусловного Б., соответствующее множеству Тпроизвольной мощности и совпадающее с ним при 
 , - семейство
, - семейство  такое, что для любого элемента
такое, что для любого элемента  существует семейство линейных комбинаций (частичных сумм) элементов из А, называемое обобщенным разложением х, суммируемое к х:для любой окрестности нуля
существует семейство линейных комбинаций (частичных сумм) элементов из А, называемое обобщенным разложением х, суммируемое к х:для любой окрестности нуля  найдется конечное подмножество
найдется конечное подмножество  такое, что для каждого конечного множества
такое, что для каждого конечного множества  имеет место
имеет место

т. е. когда частичные суммы образуют систему (фильтр) Коши. Так, напр., любой ортонормированный Б. гильбертова пространства является суммирующим Б. Аналогично определяется слабый суммирующий базис. Вполне суммирующий базис- такой суммирующий Б., что существует ограниченное множестве Втакое, что множество полунорм  суммируемо. Вполне суммирующий Б. не более чем сче-тен. В дуально ядерном пространстве каждый слабо суммирующий Б. вполне суммирующий.
суммируемо. Вполне суммирующий Б. не более чем сче-тен. В дуально ядерном пространстве каждый слабо суммирующий Б. вполне суммирующий.
Базис абсолютный (абсолютно суммирующий базис) - суммирующий Б. локально выпуклого пространства над нормированным полем такой, что для каждой окрестности нуля  и для каждого
и для каждого  суммируемо семейство полунорм
суммируемо семейство полунорм  Всякий безусловный счетный Б. абсолютен, т. е. ряд
Всякий безусловный счетный Б. абсолютен, т. е. ряд  сходится для всех
сходится для всех  и всех непрерывных полунорм
и всех непрерывных полунорм  . Среди банаховых пространств абсолютным счетным Б. обладают только пространства l1. Если пространство Фреше имеет абсолютный Б., то все его безусловные Б. абсолютны. В ядерных пространствах Фреше каждый счетный Б. (если он существует) абсолютный [13].
. Среди банаховых пространств абсолютным счетным Б. обладают только пространства l1. Если пространство Фреше имеет абсолютный Б., то все его безусловные Б. абсолютны. В ядерных пространствах Фреше каждый счетный Б. (если он существует) абсолютный [13].
Базис Шаудера - Б.  пространства Xтакой, что определенное им Оазисное отображение непрерывно [и, следовательно, является изоморфизмом на нек-рое пространство К(Т)], т. е. Б., в к-ром компоненты
пространства Xтакой, что определенное им Оазисное отображение непрерывно [и, следовательно, является изоморфизмом на нек-рое пространство К(Т)], т. е. Б., в к-ром компоненты  для любого
для любого  и, в частности, коэффициенты разложения
и, в частности, коэффициенты разложения  по этому Б., являются непрерывными функционалами на
по этому Б., являются непрерывными функционалами на  . Определен впервые Ю. Шаудером [5] для случая
. Определен впервые Ю. Шаудером [5] для случая  . Понятие базиса Шаудера является важнейшим среди всех модификаций понятия Б.
. Понятие базиса Шаудера является важнейшим среди всех модификаций понятия Б.
Базис Шаудера Характеризуется тем, что  и
и  образуют биортогональную систему. Напр., в пространствах
образуют биортогональную систему. Напр., в пространствах  последовательности
последовательности  образуют счетный базис Шаудера. В пространстве
образуют счетный базис Шаудера. В пространстве  счетный базис Шаудера образует Хаара система. В полных метрич. векторных (в частности, банаховых) пространствах всякий счетный Б. является базисом Шаудера [10]. В пространствах Фреше понятия слабого Б. и базиса Шаудера совпадают [11]. В бочечных пространствах, в к-рых нет вообще линейных непрерывных функционалов [8], не существует и базиса Шаудера. Однако, если в них существует слабый базис Шаудера, то он является (обычным) базисом Шаудера [9]. Рефлексивность бочечного локально выпуклого пространства со счетным базисом Шаудера имеет место тогда и только тогда, когда этот Б. является одновременно натягивающим, т. е. если для него
счетный базис Шаудера образует Хаара система. В полных метрич. векторных (в частности, банаховых) пространствах всякий счетный Б. является базисом Шаудера [10]. В пространствах Фреше понятия слабого Б. и базиса Шаудера совпадают [11]. В бочечных пространствах, в к-рых нет вообще линейных непрерывных функционалов [8], не существует и базиса Шаудера. Однако, если в них существует слабый базис Шаудера, то он является (обычным) базисом Шаудера [9]. Рефлексивность бочечного локально выпуклого пространства со счетным базисом Шаудера имеет место тогда и только тогда, когда этот Б. является одновременно натягивающим, т. е. если для него  будет Б. в сопряженном пространстве
будет Б. в сопряженном пространстве  , и ограниченно полным, т. е. если ограниченность множества частных сумм ряда
, и ограниченно полным, т. е. если ограниченность множества частных сумм ряда  влечет сходимость этого ряда [12]. Если базис Шаудера является безусловным Б. в банаховом пространстве, то он тогда и только тогда является натягивающим (соответственно ограниченно полным), когда в Xнет подпространств, изоморфных
влечет сходимость этого ряда [12]. Если базис Шаудера является безусловным Б. в банаховом пространстве, то он тогда и только тогда является натягивающим (соответственно ограниченно полным), когда в Xнет подпространств, изоморфных  (соответственно с 0).
(соответственно с 0).
Базис Шаудера в локально выпуклом пространстве равностепенно непрерывен, если для каждой окрестности нуля Uнайдется окрестность нуля Vтакая, что  для всех
для всех  . Каждый базис Шаудера бочечного пространства равностепенно непрерывен, и каждое полное локально выпуклое пространство со счетным равностепенно непрерывным Б. отождествимо с некоторым пространством последовательностей [15]. Равностепенно непрерывный Б. ядерного пространства абсолютен.
. Каждый базис Шаудера бочечного пространства равностепенно непрерывен, и каждое полное локально выпуклое пространство со счетным равностепенно непрерывным Б. отождествимо с некоторым пространством последовательностей [15]. Равностепенно непрерывный Б. ядерного пространства абсолютен.
Лит.: [1] Кон П., Универсальная алгебра, пер. с англ., М., 1968; [2] Мальцев А. И., Алгебраические системы, М., 1970; [3] Бурбаки Н., Алгебра. Алгебраические структуры. Линейная и полилинейная алгебра, пер. с франц., М., 1962; [4] Ham el G., "Math. Ann.", 1905, Bd 60, S. 459-62; [5] Sсhaudеr J., "Math. Z.", 1927, Bd 26, S. 47-65, 417-31; [6] Энфло П., "Математика", 1974, т. 18, № 1, с. 146- 155; [7] Зобин Н. М., Митягин Б. С., "Функциональный анализ и его приложения", 1974, т. 8, № 4, с. 35 - 47; [8] Эдвардс Р. <Э., Функциональный анализ, пер. с англ., М., 1969; [9] Diеudоnne J., "Arch. Math.", 1951, Bd 1, S.81 - 115; [10] Arsov M. G., "Pacific J. Math.", I960, t. 10, p. 365-79; [11] Bessaga C., Pelezynski A., "Studia Math.", 1960, v. 19, p. 53-62; [12] James R. C., "Ann. Math.", 1950, V. 52, № 2, p. 518-27; [13] Дынин А. С., Митягин Б. С., "Bull. Acad. Polon. Sci.", (Ser. Sci math.), 1960, t. 8, p. 535-40; [14] Дэй М. М., Нормированные линейные пространства, пер. с англ., М., 1961;[15] Пич А., Ядерные локально выпуклые пространства, пер. с нем., М., 1967.
М. И. Войцеховский, М. И. Кадец.

 к элементам
к элементам  получается любой элемент
получается любой элемент  Это понятие связано с понятием зависимости: элементы Xпосредством операций из
Это понятие связано с понятием зависимости: элементы Xпосредством операций из  ставятся в зависимость от элементов В. Минимальность означает, что никакое собственное подмножество
ставятся в зависимость от элементов В. Минимальность означает, что никакое собственное подмножество  не порождает X. Это свойство обусловливает в нек-ром смысле независимость его элементов: никакой элемент
не порождает X. Это свойство обусловливает в нек-ром смысле независимость его элементов: никакой элемент  не порождается остальными его элементами. Напр., множество всех натуральных чисел
не порождается остальными его элементами. Напр., множество всех натуральных чисел  имеет Б. единствевг-ный элемент 0 и порождается из него операцией непосредственного следования и ее итерациями; множество всех натуральных чисел
имеет Б. единствевг-ный элемент 0 и порождается из него операцией непосредственного следования и ее итерациями; множество всех натуральных чисел  порождается операцией умножения из Б., состоящего из всех простых чисел. Базис алгебры кватернионов состоит из четырех элементов
порождается операцией умножения из Б., состоящего из всех простых чисел. Базис алгебры кватернионов состоит из четырех элементов  если порождающими операциями являются сложение и умножение на действительные числа; если же кроме этих операций используется еще и умножение кватернионов, то Б. будет состоять лишь из трех элементов
если порождающими операциями являются сложение и умножение на действительные числа; если же кроме этих операций используется еще и умножение кватернионов, то Б. будет состоять лишь из трех элементов  (ибо
(ибо  ).
). - подпоследовательность
- подпоследовательность  множества
множества  натуральных чисел с включением 0, к-рая в результате Декретного сложения с собой (операция порождения) дает все
натуральных чисел с включением 0, к-рая в результате Декретного сложения с собой (операция порождения) дает все  Это означает, что каждое натуральное число ппредставимо в виде
Это означает, что каждое натуральное число ппредставимо в виде 
 Напр., всякое натуральное число есть сумма четырех квадратов натуральных чисел (теорема Лагранжа), т. е. последовательность квадратов есть Б.
Напр., всякое натуральное число есть сумма четырех квадратов натуральных чисел (теорема Лагранжа), т. е. последовательность квадратов есть Б.  порядка 4. Вообще, последовательность
порядка 4. Вообще, последовательность  степеней натуральных чисел является Б.
степеней натуральных чисел является Б.  (теорема Гильберта), порядок к-рого оценивается Виноградова методом. Понятие Б.
(теорема Гильберта), порядок к-рого оценивается Виноградова методом. Понятие Б.  обобщается на случай произвольных числовых последовательностей, т. е. функций на
обобщается на случай произвольных числовых последовательностей, т. е. функций на  .
. множества существуют всегда (тривиально:
множества существуют всегда (тривиально:  порождает
порождает  ), однако минимальность может оказаться принципиально невозможной (подобная ситуация типична для классов
), однако минимальность может оказаться принципиально невозможной (подобная ситуация типична для классов  , содержащих бес-конечноместные операции, в частности в топологич. структурах, решетках и т. п.). Поэтому условие минимальности заменяется более слабым требованием: Б. есть порождающее множество минимальной мощности. В связи с этим обычно
, содержащих бес-конечноместные операции, в частности в топологич. структурах, решетках и т. п.). Поэтому условие минимальности заменяется более слабым требованием: Б. есть порождающее множество минимальной мощности. В связи с этим обычно  . Вопределяется как параметризованное множество (или семейство), т. е. как функция
. Вопределяется как параметризованное множество (или семейство), т. е. как функция  на множестве индексов
на множестве индексов  со значениями в
со значениями в  , причем
, причем  ; мощность Тиногда наз. базисной размерностью (или рангом)
; мощность Тиногда наз. базисной размерностью (или рангом) Напр., счетное всюду плотное множество
Напр., счетное всюду плотное множество  сепарабель-ного топологич. пространства
сепарабель-ного топологич. пространства  можно считать его
можно считать его  .;
.;  порождается из
порождается из  операцией замыкания (к-рая, кстати, и в более общих случаях родственна порождению, см. ниже).
операцией замыкания (к-рая, кстати, и в более общих случаях родственна порождению, см. ниже). (база) - Б.
(база) - Б.  совокупности всех открытых подмножеств X;порождение осуществляется объединением элементов
совокупности всех открытых подмножеств X;порождение осуществляется объединением элементов 
 (двойственный базе
(двойственный базе  в смысле Тарского) - плотное множество (минимальной мощности)
в смысле Тарского) - плотное множество (минимальной мощности)  в
в  ; порождение
; порождение  из
из  (а тем самым и само
(а тем самым и само  ) определяется условием
) определяется условием  (что равносильно
(что равносильно  ), где
), где  ,
,  ,
,  - единица
- единица  ,
,  - операция импликации. Аналогично вводится ибазис фильтра
- операция импликации. Аналогично вводится ибазис фильтра  , как множество
, как множество  такое, что для любого
такое, что для любого  существует
существует  , и
, и  .
. вводится по следующей схеме. Пусть
вводится по следующей схеме. Пусть 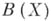 - булеан
- булеан  , т. е. совокупность всех его подмножеств. Порождающим оператором (или оператором замыкания)
, т. е. совокупность всех его подмножеств. Порождающим оператором (или оператором замыкания)  называется отображение
называется отображение  в себя такое, что: если
в себя такое, что: если 

 порождается множеством
порождается множеством  , если
, если  в частности,
в частности, порождает
порождает  , если
, если 
 . Минимальное множество
. Минимальное множество  , обладающее этим свойством, и наз. базисом
, обладающее этим свойством, и наз. базисом  .определенным оператором
.определенным оператором  . Порождающий оператор J имеет конечный тип, если для любых
. Порождающий оператор J имеет конечный тип, если для любых  из
из  следует
следует  для нек-рого конечного подмножества
для нек-рого конечного подмножества  порождающий оператор
порождающий оператор  обладает свойством замещения, если для любых
обладает свойством замещения, если для любых  следует
следует  Порождающий оператор
Порождающий оператор  конечного типа со свойством замещения определяет на X отношение зависимости, т. е. разбиение
конечного типа со свойством замещения определяет на X отношение зависимости, т. е. разбиение  на два класса - зависимых и независимых множеств; множество Аназ. зависимым, если
на два класса - зависимых и независимых множеств; множество Аназ. зависимым, если  для нек-рого
для нек-рого  , и независимым, если
, и независимым, если  для любого
для любого  . При этом
. При этом  зависимо (независимо) тогда и только тогда, когда некоторое (любое) непустое конечное подмножество
зависимо (независимо) тогда и только тогда, когда некоторое (любое) непустое конечное подмножество  зависимо (независимо).
зависимо (независимо). было Б. множества
было Б. множества  , необходимо н достаточно, чтобы
, необходимо н достаточно, чтобы  было независимым порождающим
было независимым порождающим  множеством или, иначе, максимальным независимым в
множеством или, иначе, максимальным независимым в  множеством.
множеством. - произвольное независимое множество, а С - порождающее
- произвольное независимое множество, а С - порождающее  множество, содержащее А, то существует Б. Вв X такой, что
множество, содержащее А, то существует Б. Вв X такой, что  В частности, Xвсегда обладает Б., и любые два его Б. равно-мощны.
В частности, Xвсегда обладает Б., и любые два его Б. равно-мощны. в любую алгебраич. систему
в любую алгебраич. систему  (той же сигнатуры) может быть продолжено до (гомо) морфизма
(той же сигнатуры) может быть продолжено до (гомо) морфизма  в
в  , пли, что то же самое, для любого (гомо)морфизма
, пли, что то же самое, для любого (гомо)морфизма  и любого множества
и любого множества  порождающие операторы
порождающие операторы  удовлетворяют условию:
удовлетворяют условию:
 элементов K-модуля Мназ. свободным, если из
элементов K-модуля Мназ. свободным, если из  (где
(где  для всех, кроме конечного числа индексов
для всех, кроме конечного числа индексов  следует
следует  для всех
для всех  , а порождение осуществляется представлением элементов хв виде линейных комбинаций элементов
, а порождение осуществляется представлением элементов хв виде линейных комбинаций элементов  : существует (зависящее от х).множество элементов
: существует (зависящее от х).множество элементов  такое, что
такое, что  для всех, кроме конечного числа индексов t, и имеет место разложение
для всех, кроме конечного числа индексов t, и имеет место разложение 
 одного комплексного переменного, являющееся дискретной абелевой группой (и потому модулем над кольцом
одного комплексного переменного, являющееся дискретной абелевой группой (и потому модулем над кольцом  ). имеет свободный Б., наз. базисом периодов функции
). имеет свободный Б., наз. базисом периодов функции  ; он состоит из двух так наз. примитивных периодов. Аналогично определяется Б. периодов абелевой функции нескольких комплексных переменных.
; он состоит из двух так наз. примитивных периодов. Аналогично определяется Б. периодов абелевой функции нескольких комплексных переменных. представим линейной комбинацией элементов Б. единственным образом. Элементы
представим линейной комбинацией элементов Б. единственным образом. Элементы  , являющиеся линейными функционалами на X, наз. компонентами (координатами)
, являющиеся линейными функционалами на X, наз. компонентами (координатами)  в данном Б.
в данном Б. .
.
 , если
, если  - значение t-й компоненты хв Б. A и 0 в противном случае, наз. базисным отображением; оно является линейным инъективным отображением Xв пространство
- значение t-й компоненты хв Б. A и 0 в противном случае, наз. базисным отображением; оно является линейным инъективным отображением Xв пространство  функций на Тсо значениями в K. В данном случае образ
функций на Тсо значениями в K. В данном случае образ  состоит из функций с конечным числом значений, отличных от нуля (конечнозначных функций). Эта интерпретация позволяет определить обобщенный базис векторного пространства
состоит из функций с конечным числом значений, отличных от нуля (конечнозначных функций). Эта интерпретация позволяет определить обобщенный базис векторного пространства  над полем
над полем  как биективное линейное отображение его на нек-рое подпространство
как биективное линейное отображение его на нек-рое подпространство  пространства
пространства  функций на
функций на  со значениями в
со значениями в  , где
, где  - нек-рое надлежащим образом подобранное множество. Однако без введения дополнительных ограничений на
- нек-рое надлежащим образом подобранное множество. Однако без введения дополнительных ограничений на  (напр., порядка) и структур на
(напр., порядка) и структур на  (напр., топологии) и согласованных с этим условий на
(напр., топологии) и согласованных с этим условий на  понятие обобщенного Б. практически мало полезно.
понятие обобщенного Б. практически мало полезно. наз. алгебраическим базисом (чем подчеркивается отсутствие связи с дополнительными структурами на
наз. алгебраическим базисом (чем подчеркивается отсутствие связи с дополнительными структурами на  , даже если они и согласованы с его векторной структурой).
, даже если они и согласованы с его векторной структурой). ; график решения его всюду плотен на плоскости
; график решения его всюду плотен на плоскости  . Каждой почти периодич. функции
. Каждой почти периодич. функции  соответствует нек-рый счетный базис Гамеля
соответствует нек-рый счетный базис Гамеля  такой, что каждый показатель Фурье
такой, что каждый показатель Фурье  этой функции принадлежит линейной оболочке
этой функции принадлежит линейной оболочке  . При этом элементы
. При этом элементы  можно выбрать принадлежащими последовательности
можно выбрать принадлежащими последовательности  ; множество
; множество  наз. базисом почтп периодической функции. Аналогичный Б. строится в кольце, содержащем тело Ри имеющем единицу тела Рсвоей единицей. Алгебраич. Б. произвольного векторного пространства также наз. иногда базисом Гамеля.
наз. базисом почтп периодической функции. Аналогичный Б. строится в кольце, содержащем тело Ри имеющем единицу тела Рсвоей единицей. Алгебраич. Б. произвольного векторного пространства также наз. иногда базисом Гамеля. , свойства и функции к-рого аналогичны свойствам н функциям алгебраич. Б. векторного пространства. Понятие топологич. В.- одно из важнейших в функциональном анализе - расширяет и углубляет понятие алгебраич. Б. с учетом топологич. структуры X и позволяет получать для каждого элемента
, свойства и функции к-рого аналогичны свойствам н функциям алгебраич. Б. векторного пространства. Понятие топологич. В.- одно из важнейших в функциональном анализе - расширяет и углубляет понятие алгебраич. Б. с учетом топологич. структуры X и позволяет получать для каждого элемента  его разложение по Б.
его разложение по Б.  и притом единственное, т. е. представление хв виде предела (в том или ином смысле) линейных комбинаций элементов
и притом единственное, т. е. представление хв виде предела (в том или ином смысле) линейных комбинаций элементов  :
: где
где  - линейные функционалы на Xсо значениями в К, наз. компонентами х в Б . А, или коэффициентами разложениям по Б. А. Очевидно, для существования разложения любого хнеобходимо, чтобы Абыло полным множеством в X, а для единственности такого разложения (т. е. для того, чтобы нулевой элемент Xимел все компоненты равными нулю) необходимо, чтобы Абыло топологическим свободным множеством в X.
- линейные функционалы на Xсо значениями в К, наз. компонентами х в Б . А, или коэффициентами разложениям по Б. А. Очевидно, для существования разложения любого хнеобходимо, чтобы Абыло полным множеством в X, а для единственности такого разложения (т. е. для того, чтобы нулевой элемент Xимел все компоненты равными нулю) необходимо, чтобы Абыло топологическим свободным множеством в X. , на нек-рое, зависящее от X, пространство
, на нек-рое, зависящее от X, пространство  функций со значениями в К, определенных на (топологическом) пространстве Т, а именно:
функций со значениями в К, определенных на (топологическом) пространстве Т, а именно:
 , так что символически
, так что символически  и
и  ; при этом строение
; при этом строение  вследствие конкретности, эффективности своего определения проще и обозримее, чем строение абстрактно заданного
вследствие конкретности, эффективности своего определения проще и обозримее, чем строение абстрактно заданного  . Так, напр., алгебраич. Б. бесконечномерного банахова пространства несчетен, в то время как в ряде случаев при надлежащем обобщении понятия Б. мощность
. Так, напр., алгебраич. Б. бесконечномерного банахова пространства несчетен, в то время как в ряде случаев при надлежащем обобщении понятия Б. мощность  существенно уменьшается, одновременно упрощается и
существенно уменьшается, одновременно упрощается и  .
. содержит все конечнозначные функции, и множество элементов Б.
содержит все конечнозначные функции, и множество элементов Б.  является биективным прообразом множества функций
является биективным прообразом множества функций  , имеющих лишь одно ненулевое значение, равное 1 ("однозначных" функций):
, имеющих лишь одно ненулевое значение, равное 1 ("однозначных" функций): где
где  при
при  . Другими словами,
. Другими словами, - образующая одномерного подпространства
- образующая одномерного подпространства  , дополнительного в Xк гиперплоскости, определяемой уравнением
, дополнительного в Xк гиперплоскости, определяемой уравнением 
 сводится к организации из множества компонент
сводится к организации из множества компонент  , составляющих образ хпри базисном отображении, суммируемого (в том или ином смысле) семейства
, составляющих образ хпри базисном отображении, суммируемого (в том или ином смысле) семейства  , т. е. Б. "разлагает" пространство Xв (обобщенную) прямую сумму одномерных подпространств:
, т. е. Б. "разлагает" пространство Xв (обобщенную) прямую сумму одномерных подпространств:
 , близостной и другими дополнительными структурами.
, близостной и другими дополнительными структурами. элементов пространства Xтакая, что каждому элементу ходнозначно соответствует разложение его в ряд по Б.
элементов пространства Xтакая, что каждому элементу ходнозначно соответствует разложение его в ряд по Б.

 причем существен естественный порядок в нем. Часто счетный Б. наз. просто Б. [Аналогично, если подразумевается слабая сходимость разложения х, определяется слабый счетный базис.] Так, напр., функции
причем существен естественный порядок в нем. Часто счетный Б. наз. просто Б. [Аналогично, если подразумевается слабая сходимость разложения х, определяется слабый счетный базис.] Так, напр., функции  ,
,  образуют Б. в пространствах
образуют Б. в пространствах  (абсолютно суммируемых в степени рпериодич. функций), напротив, в пространствах
(абсолютно суммируемых в степени рпериодич. функций), напротив, в пространствах  (измеримых функций, совпадающих почти всюду с ограниченными функциями) и
(измеримых функций, совпадающих почти всюду с ограниченными функциями) и  (непрерывных периодич. функций) эти функции Б. не образуют. Необходимым (но далеко не достаточным) условием существования счетного Б. является сепарабельность
(непрерывных периодич. функций) эти функции Б. не образуют. Необходимым (но далеко не достаточным) условием существования счетного Б. является сепарабельность  (напр., в пространстве измеримых на отрезке
(напр., в пространстве измеримых на отрезке  функций со значениями в
функций со значениями в  счетного Б. быть не может). Впрочем, пространство
счетного Б. быть не может). Впрочем, пространство  ограниченных последовательностей, не будучи сепарабельным в топологии
ограниченных последовательностей, не будучи сепарабельным в топологии  , не обладает счетным Б., однако элементы
, не обладает счетным Б., однако элементы 
 , где
, где  при
при  и
и  при
при  , образуют Б. в слабой топологии
, образуют Б. в слабой топологии  . Вопрос о существовании счетного Б. в сепарабельных банаховых пространствах (проблема базиса) решен отрицательно [6]. Аналогичный вопрос для ядерных пространств также решен отрицательно [7].
. Вопрос о существовании счетного Б. в сепарабельных банаховых пространствах (проблема базиса) решен отрицательно [6]. Аналогичный вопрос для ядерных пространств также решен отрицательно [7]. не являются непрерывными, разложение
не являются непрерывными, разложение  не сходится безусловно и т. п.), в связи с чем на Б. накладываются некоторые условия или вводится надлежащее его обобщение.
не сходится безусловно и т. п.), в связи с чем на Б. накладываются некоторые условия или вводится надлежащее его обобщение. и несчетно, но разложение элемента
и несчетно, но разложение элемента  по нему естественно определяется: соответствующее пространство
по нему естественно определяется: соответствующее пространство  состоит из счетнозначных функций. Напр., полное орто-нормированное множество
состоит из счетнозначных функций. Напр., полное орто-нормированное множество  в гильбертовом пространстве Нявляется Б.; если
в гильбертовом пространстве Нявляется Б.; если  , то
, то  (где
(где  - скалярное произведение в Н).для всех, за исключением быть может счетного множества, индексов
- скалярное произведение в Н).для всех, за исключением быть может счетного множества, индексов  , и ряд
, и ряд  сходится к х. Базисное отображение определяется ортогональным проектированием на замкнутые подпространства, порожденные элементами
сходится к х. Базисное отображение определяется ортогональным проектированием на замкнутые подпространства, порожденные элементами  Б. пространства
Б. пространства  всех комплекснозначных почти периодич. функций на
всех комплекснозначных почти периодич. функций на  состоит из функций
состоит из функций  ; здесь
; здесь  - совокупность счетнозначных функций, а базисное отображение определяется формулой
- совокупность счетнозначных функций, а базисное отображение определяется формулой 
 (последовательностей, сходящихся к нулю) и
(последовательностей, сходящихся к нулю) и  (последовательностей, суммирую мых в степени
(последовательностей, суммирую мых в степени  ) элементы
) элементы  образуют безусловный Б.; в пространстве
образуют безусловный Б.; в пространстве  непрерывных на отрезке
непрерывных на отрезке  функций (любой) Б. не может быть безусловным. Ортонормированный счетный Б. гильбертова пространства - безусловный Б. Банахово пространство с безусловным Б. слабо полно (соответственно обладает сепарабельным сопряженным пространством) в том и только в том случае, когда оно не содержит подпространства, изоморфного с 0 (соответственно
функций (любой) Б. не может быть безусловным. Ортонормированный счетный Б. гильбертова пространства - безусловный Б. Банахово пространство с безусловным Б. слабо полно (соответственно обладает сепарабельным сопряженным пространством) в том и только в том случае, когда оно не содержит подпространства, изоморфного с 0 (соответственно  ).
). и
и  соответствующих банаховых пространств Xи Yназ. эквивалентными, если существует биективное линейное отображение Т:
соответствующих банаховых пространств Xи Yназ. эквивалентными, если существует биективное линейное отображение Т: , распространяемое до изоморфизма Xв Y;эти Б. наз. квазиэквивалентными, если они становятся эквивалентными после нек-рой перестановки и нормировки элементов одного из них. Пространства
, распространяемое до изоморфизма Xв Y;эти Б. наз. квазиэквивалентными, если они становятся эквивалентными после нек-рой перестановки и нормировки элементов одного из них. Пространства  обладают тем свойством, что в каждом из них все нормированные безусловные Б. эквивалентны. В декартовом произведении
обладают тем свойством, что в каждом из них все нормированные безусловные Б. эквивалентны. В декартовом произведении  квазиэквивалентны все безусловные Б. Существуют, однако, нормированные Б., не эквивалентные ортонормированному.
квазиэквивалентны все безусловные Б. Существуют, однако, нормированные Б., не эквивалентные ортонормированному.
 , - семейство
, - семейство  такое, что для любого элемента
такое, что для любого элемента  существует семейство линейных комбинаций (частичных сумм) элементов из А, называемое обобщенным разложением х, суммируемое к х:для любой окрестности нуля
существует семейство линейных комбинаций (частичных сумм) элементов из А, называемое обобщенным разложением х, суммируемое к х:для любой окрестности нуля  найдется конечное подмножество
найдется конечное подмножество  такое, что для каждого конечного множества
такое, что для каждого конечного множества  имеет место
имеет место 
 суммируемо. Вполне суммирующий Б. не более чем сче-тен. В дуально ядерном пространстве каждый слабо суммирующий Б. вполне суммирующий.
суммируемо. Вполне суммирующий Б. не более чем сче-тен. В дуально ядерном пространстве каждый слабо суммирующий Б. вполне суммирующий. и для каждого
и для каждого  суммируемо семейство полунорм
суммируемо семейство полунорм  Всякий безусловный счетный Б. абсолютен, т. е. ряд
Всякий безусловный счетный Б. абсолютен, т. е. ряд  сходится для всех
сходится для всех  и всех непрерывных полунорм
и всех непрерывных полунорм  . Среди банаховых пространств абсолютным счетным Б. обладают только пространства l1. Если пространство Фреше имеет абсолютный Б., то все его безусловные Б. абсолютны. В ядерных пространствах Фреше каждый счетный Б. (если он существует) абсолютный [13].
. Среди банаховых пространств абсолютным счетным Б. обладают только пространства l1. Если пространство Фреше имеет абсолютный Б., то все его безусловные Б. абсолютны. В ядерных пространствах Фреше каждый счетный Б. (если он существует) абсолютный [13]. пространства Xтакой, что определенное им Оазисное отображение непрерывно [и, следовательно, является изоморфизмом на нек-рое пространство К(Т)], т. е. Б., в к-ром компоненты
пространства Xтакой, что определенное им Оазисное отображение непрерывно [и, следовательно, является изоморфизмом на нек-рое пространство К(Т)], т. е. Б., в к-ром компоненты  для любого
для любого  и, в частности, коэффициенты разложения
и, в частности, коэффициенты разложения  по этому Б., являются непрерывными функционалами на
по этому Б., являются непрерывными функционалами на  . Определен впервые Ю. Шаудером [5] для случая
. Определен впервые Ю. Шаудером [5] для случая  . Понятие базиса Шаудера является важнейшим среди всех модификаций понятия Б.
. Понятие базиса Шаудера является важнейшим среди всех модификаций понятия Б. и
и  образуют биортогональную систему. Напр., в пространствах
образуют биортогональную систему. Напр., в пространствах  последовательности
последовательности  образуют счетный базис Шаудера. В пространстве
образуют счетный базис Шаудера. В пространстве  счетный базис Шаудера образует Хаара система. В полных метрич. векторных (в частности, банаховых) пространствах всякий счетный Б. является базисом Шаудера [10]. В пространствах Фреше понятия слабого Б. и базиса Шаудера совпадают [11]. В бочечных пространствах, в к-рых нет вообще линейных непрерывных функционалов [8], не существует и базиса Шаудера. Однако, если в них существует слабый базис Шаудера, то он является (обычным) базисом Шаудера [9]. Рефлексивность бочечного локально выпуклого пространства со счетным базисом Шаудера имеет место тогда и только тогда, когда этот Б. является одновременно натягивающим, т. е. если для него
счетный базис Шаудера образует Хаара система. В полных метрич. векторных (в частности, банаховых) пространствах всякий счетный Б. является базисом Шаудера [10]. В пространствах Фреше понятия слабого Б. и базиса Шаудера совпадают [11]. В бочечных пространствах, в к-рых нет вообще линейных непрерывных функционалов [8], не существует и базиса Шаудера. Однако, если в них существует слабый базис Шаудера, то он является (обычным) базисом Шаудера [9]. Рефлексивность бочечного локально выпуклого пространства со счетным базисом Шаудера имеет место тогда и только тогда, когда этот Б. является одновременно натягивающим, т. е. если для него  будет Б. в сопряженном пространстве
будет Б. в сопряженном пространстве  , и ограниченно полным, т. е. если ограниченность множества частных сумм ряда
, и ограниченно полным, т. е. если ограниченность множества частных сумм ряда  влечет сходимость этого ряда [12]. Если базис Шаудера является безусловным Б. в банаховом пространстве, то он тогда и только тогда является натягивающим (соответственно ограниченно полным), когда в Xнет подпространств, изоморфных
влечет сходимость этого ряда [12]. Если базис Шаудера является безусловным Б. в банаховом пространстве, то он тогда и только тогда является натягивающим (соответственно ограниченно полным), когда в Xнет подпространств, изоморфных  (соответственно с 0).
(соответственно с 0). для всех
для всех  . Каждый базис Шаудера бочечного пространства равностепенно непрерывен, и каждое полное локально выпуклое пространство со счетным равностепенно непрерывным Б. отождествимо с некоторым пространством последовательностей [15]. Равностепенно непрерывный Б. ядерного пространства абсолютен.
. Каждый базис Шаудера бочечного пространства равностепенно непрерывен, и каждое полное локально выпуклое пространство со счетным равностепенно непрерывным Б. отождествимо с некоторым пространством последовательностей [15]. Равностепенно непрерывный Б. ядерного пространства абсолютен.