|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ,Значение ОБРАТНЫЕ ТРИГОНОМЕТРИЧЕСКИЕ ФУНКЦИИ, в математической энциклопедии: аркфуикции, круговые функции,- функции, обратные тригонометрическим функциям. Шести основным тригонометрич. функциям соответствуют шесть О. т. ф.: арксинус, арккосинус, арктангенс, арккотангенс, арксеканс, арккосеканс; обозначаются соответственно Arc sin х,Arc cos x,Arc tg x,Arc ctg x,Arc sec x,Arc cosec x. Функции Arc sin xи Arc cos xопределены (в действительной области) для Так как тригонометрич. функции периодические, то обратные к ним функции являются многозначными функциями. Определенные однозначные ветви (главные ветви) этих функции обозначаются так: arc sin х,arc cos x, ... Именно, arc sin xесть та ветвь функции Arc sin x, для к-рой
На рисунке изображены графики функций у= Аrс sin х, у= Аrсcos, x, у=Arc tg x, y=Arc ctg x ', главные ветви этих функций выделены жирной линией. О. т. ф. Arc sin x, . . . легко выражаются через arc sin x, . .., напр.:
О. т. ф. связаны соотношениями
Поэтому функции О. т. ф. бесконечно дифференцируемы и в окрестности каждой внутренней точки своей области определения могут быть разложены в ряды Тейлора. Производные, интегралы и разложения в ряды О. т. ф.:
О. т. ф. комплексного переменного определяются как аналитические продолжения соответствующих О. т. ф. действительного переменного в комплексную плоскость. О. т. ф. выражаются через логарифмическую функцию:
Ю. В. Сидоров. |
|
|
|
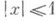, функции Arc tg x и Arc ctg x- для всех действительных х, а функции Arc sec xи Arc cosec x- для 
; две последние функции малоупотребительны. Другие обозначения:
и т. п.
Аналогично, функции arc cos x,arc tg хи arc ctg xопределяются из условий: 
, 
.
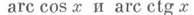в нижеследующих формулах не фигурируют.
