|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ОБОБЩЕННОЙ ФУНКЦИИ ПРОИЗВОДНАЯЗначение ОБОБЩЕННОЙ ФУНКЦИИ ПРОИЗВОДНАЯ в математической энциклопедии: - слабое расширение операции обычного дифференцирования. Пусть обобщенная функция
порядка
Так как операция Имеют место следующие свойства О. ф. п.: операция Пусть Примеры. 1) 2) Общее решение уравнения 3) Тригонометрический ряд
сходится в D' и его можно дифференцировать в D' почленно бесконечное число раз. Лит.:[1] Schwartz L., Theorie des distributions, v. 1, P., 1950; [2] Соболев С. Л., Некоторые применения функционального анализа в математической физике, Новосиб., 1962, В. С. Владимиров. |
|
|
|

 . Обобщенная (слабая) производная
. Обобщенная (слабая) производная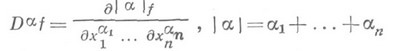
 определяется равенством
определяется равенством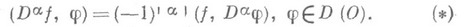
 линейна и непрерывна из D(О)в D(О), то функционал
линейна и непрерывна из D(О)в D(О), то функционал  определяемый правой частью равенства (*), есть обобщенная функция из
определяемый правой частью равенства (*), есть обобщенная функция из  . Если
. Если  при всех
при всех  таких, что
таких, что 
 линейна и непрерывна из D' (О)в D' (О);любая обобщенная функция из D' (О)бесконечно дифференцируема (в обобщенном смысле); дифференцирование He-зависит от порядка; справедлива формула Лейбница для дифференцирования произведения аf, где
линейна и непрерывна из D' (О)в D' (О);любая обобщенная функция из D' (О)бесконечно дифференцируема (в обобщенном смысле); дифференцирование He-зависит от порядка; справедлива формула Лейбница для дифференцирования произведения аf, где 
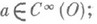
 Может случиться, что нек-рая обобщенная производная
Может случиться, что нек-рая обобщенная производная  может быть отождествлена с нек-рой
может быть отождествлена с нек-рой  (О)-функцией. В этом случае
(О)-функцией. В этом случае  - обобщенная производная типа функции.
- обобщенная производная типа функции. где
где  - функция Хевисайда и d - функция Дирака.
- функция Хевисайда и d - функция Дирака. в классе
в классе  есть произвольная постоянная.
есть произвольная постоянная.