"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ОБОБЩЕННАЯ ПРОИЗВОДНАЯ
Значение ОБОБЩЕННАЯ ПРОИЗВОДНАЯ в математической энциклопедии:
типа функции - распространение понятия производной на некоторые классы недифференцируемых функций. Первое определение принадлежит С. Л. Соболеву (см. [1], [2]), к-рый подошел к определению О. п. с точки зрения идеи введенного им понятия обобщенной функции.
Пусть 
 - локально интегрируемые функции на открытом множестве
- локально интегрируемые функции на открытом множестве  n-мерного пространства
n-мерного пространства  , т. е. интегрируемые по Лебегу на любом замкнутом ограниченном множестве
, т. е. интегрируемые по Лебегу на любом замкнутом ограниченном множестве  . Тогда
. Тогда  есть обобщенная частная производная от fпо xj на
есть обобщенная частная производная от fпо xj на  и пишут
и пишут  , если для любой бесконечно дифференцируемой функции
, если для любой бесконечно дифференцируемой функции  , финитной в
, финитной в  (см. Финитная функция),
(см. Финитная функция),

Второе эквивалентное определение О. п. заключается в следующем. Если f можно видоизменить на множестве re-мерной меры нуль так, что видоизмененная функция (к-рая снова обозначается через f) будет локально абсолютно непрерывной по х j почти для всех (в смысле (п-1)-мерной меры) x j=(x1 . . ., xj-1 , xj + 1 , . .., х п), принадлежащих к проекции
заключается в следующем. Если f можно видоизменить на множестве re-мерной меры нуль так, что видоизмененная функция (к-рая снова обозначается через f) будет локально абсолютно непрерывной по х j почти для всех (в смысле (п-1)-мерной меры) x j=(x1 . . ., xj-1 , xj + 1 , . .., х п), принадлежащих к проекции  области
области 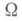 на плоскость ;
на плоскость ; , то f имеет частную (в обычном смысле этого слова) производную
, то f имеет частную (в обычном смысле этого слова) производную  почти всюду на
почти всюду на  . Если функция
. Если функция  почти всюду на
почти всюду на  , то
, то  есть О. п. от fпо
есть О. п. от fпо  на
на  . Таким образом, О. п. определена на
. Таким образом, О. п. определена на  почти всюду; если f непрерывна и имеет на
почти всюду; если f непрерывна и имеет на  непрерывную обычную производную
непрерывную обычную производную  , то последняя есть в то же время О. п. от fпо
, то последняя есть в то же время О. п. от fпо  на
на 
О. п.  высшего порядка определяются по индукции. Они не зависят (почти всюду) от порядка дифференцирования.
высшего порядка определяются по индукции. Они не зависят (почти всюду) от порядка дифференцирования.
Имеется третье эквивалентное определение О. п. Пусть для всякого замкнутого ограниченного  функции
функции  и
и  , заданные на W, обладают свойствами:
, заданные на W, обладают свойствами:

где функции  непрерывны на
непрерывны на  вместе со своими частными производными
вместе со своими частными производными  ; тогда
; тогда  есть О. п. по
есть О. п. по  от
от  на
на  (см. также Соболевапространство).
(см. также Соболевапространство).
С точки зрения теории обобщенных функций О. п. определяется следующим образом. Пусть задана функция  , локально суммируемая на
, локально суммируемая на  , рассматриваемая как обобщенная функция, и пусть
, рассматриваемая как обобщенная функция, и пусть  - частная производная в смысле теории обобщенных функций. Если окажется, что
- частная производная в смысле теории обобщенных функций. Если окажется, что  представляет локально суммируемую на
представляет локально суммируемую на  функцию, то тогда (по первому (исходному) определению)
функцию, то тогда (по первому (исходному) определению)  есть О. п.
есть О. п.
Понятие О. п. вводилось и ранее (см., напр., [3], где рассматривались О. п. с интегрируемым квадратом на  ). В дальнейшем многие исследователи приходили к этому понятию независимо от своих предшественников (см. по этому вопросу [4]).
). В дальнейшем многие исследователи приходили к этому понятию независимо от своих предшественников (см. по этому вопросу [4]).
Лит.:[1] Соболев С. Л., "Докл. АН СССР", 1935, т. 8, с. 291-94; [2] его же, "Матем. сб.", 1936, т. 1, с. 39-72; [3] Levi В., "Rend. Circolo mat. Palermo", 1906, v. 22, p. 293-359; [4] Никольский С. М., Приближение функций многих переменных и теоремы вложения, М., 1969.
С. М. Никольский.


 - локально интегрируемые функции на открытом множестве
- локально интегрируемые функции на открытом множестве  n-мерного пространства
n-мерного пространства  , т. е. интегрируемые по Лебегу на любом замкнутом ограниченном множестве
, т. е. интегрируемые по Лебегу на любом замкнутом ограниченном множестве  . Тогда
. Тогда  есть обобщенная частная производная от fпо xj на
есть обобщенная частная производная от fпо xj на  и пишут
и пишут  , если для любой бесконечно дифференцируемой функции
, если для любой бесконечно дифференцируемой функции  , финитной в
, финитной в  (см. Финитная функция),
(см. Финитная функция),
 заключается в следующем. Если f можно видоизменить на множестве re-мерной меры нуль так, что видоизмененная функция (к-рая снова обозначается через f) будет локально абсолютно непрерывной по х j почти для всех (в смысле (п-1)-мерной меры) x j=(x1 . . ., xj-1 , xj + 1 , . .., х п), принадлежащих к проекции
заключается в следующем. Если f можно видоизменить на множестве re-мерной меры нуль так, что видоизмененная функция (к-рая снова обозначается через f) будет локально абсолютно непрерывной по х j почти для всех (в смысле (п-1)-мерной меры) x j=(x1 . . ., xj-1 , xj + 1 , . .., х п), принадлежащих к проекции  области
области 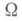 на плоскость ;
на плоскость ; , то f имеет частную (в обычном смысле этого слова) производную
, то f имеет частную (в обычном смысле этого слова) производную  почти всюду на
почти всюду на  . Если функция
. Если функция  почти всюду на
почти всюду на  , то
, то  есть О. п. от fпо
есть О. п. от fпо  на
на  . Таким образом, О. п. определена на
. Таким образом, О. п. определена на  почти всюду; если f непрерывна и имеет на
почти всюду; если f непрерывна и имеет на  непрерывную обычную производную
непрерывную обычную производную  , то последняя есть в то же время О. п. от fпо
, то последняя есть в то же время О. п. от fпо  на
на 
 высшего порядка определяются по индукции. Они не зависят (почти всюду) от порядка дифференцирования.
высшего порядка определяются по индукции. Они не зависят (почти всюду) от порядка дифференцирования. функции
функции  и
и  , заданные на W, обладают свойствами:
, заданные на W, обладают свойствами:
 непрерывны на
непрерывны на  вместе со своими частными производными
вместе со своими частными производными  ; тогда
; тогда  есть О. п. по
есть О. п. по  от
от  на
на  (см. также Соболевапространство).
(см. также Соболевапространство). , локально суммируемая на
, локально суммируемая на  , рассматриваемая как обобщенная функция, и пусть
, рассматриваемая как обобщенная функция, и пусть  - частная производная в смысле теории обобщенных функций. Если окажется, что
- частная производная в смысле теории обобщенных функций. Если окажется, что  представляет локально суммируемую на
представляет локально суммируемую на  функцию, то тогда (по первому (исходному) определению)
функцию, то тогда (по первому (исходному) определению)  есть О. п.
есть О. п. ). В дальнейшем многие исследователи приходили к этому понятию независимо от своих предшественников (см. по этому вопросу [4]).
). В дальнейшем многие исследователи приходили к этому понятию независимо от своих предшественников (см. по этому вопросу [4]).