"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
НУМЕРОВАННАЯ МОДЕЛЬ
Значение НУМЕРОВАННАЯ МОДЕЛЬ в математической энциклопедии:
- пара  , где
, где  - модель нек-рой фиксированной сигнатуры
- модель нек-рой фиксированной сигнатуры  и
и  - нумерация основного множества
- нумерация основного множества  модели
модели  Наиболее развитым направлением в изучении Н. м. является конструктивных моделей теория. Другим направлением в теории Н. м. является исследование проблемы сложности Н.. м., под к-рой понимается сложность множеств натуральных чисел
Наиболее развитым направлением в изучении Н. м. является конструктивных моделей теория. Другим направлением в теории Н. м. является исследование проблемы сложности Н.. м., под к-рой понимается сложность множеств натуральных чисел  либо множества
либо множества  . В качестве
. В качестве  здесь берется нек-рая гёделева нумерация всех формул сигнатуры
здесь берется нек-рая гёделева нумерация всех формул сигнатуры  где константы
где константы  не принадлежат сигнатуре
не принадлежат сигнатуре  - это множество всех замкнутых формул сигнатуры
- это множество всех замкнутых формул сигнатуры  истинных на системе
истинных на системе  , к-рая получается из системы
, к-рая получается из системы  обогащением сигнатуры
обогащением сигнатуры  до
до  , причем значение константы
, причем значение константы  полагает равным элементу
полагает равным элементу  означает соответственно, множество всех бескванторных предложений, истинных на системе
означает соответственно, множество всех бескванторных предложений, истинных на системе 
Различные специальные модели элементарных теорий играют важную роль в математич. логике и алгебре. Один из важных вопросов - проблема их сложности. Получены следующие результаты. Пусть  и
и  обозначают соответственно арифметическую и аналитическую иерархии относительно множества А.
обозначают соответственно арифметическую и аналитическую иерархии относительно множества А.
Если теория Трекурсивна относительно Аи имеет простую модель  , то существует нумерация
, то существует нумерация 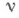 модели
модели  такая, что
такая, что  то есть
то есть  рекурсивно относительно множества
рекурсивно относительно множества  всех гёделевых номеров хтаких вычислимых относительно Афункций
всех гёделевых номеров хтаких вычислимых относительно Афункций  , для к-рых
, для к-рых  определено.
определено.
Если теория Трекурсивна относительно Аи имеет счетную насыщенную модель  , то существует нумерация
, то существует нумерация  модели
модели  такая, что
такая, что  то есть
то есть  есть гиперарифметич. множество относительно А; эти оценки сложности являются в нек-ром смысле точными.
есть гиперарифметич. множество относительно А; эти оценки сложности являются в нек-ром смысле точными.
С нахождением точной оценки связан также следующий результат. Известно, что любая непротиворечивая формула .имеет Н. м.  сложности
сложности  , т. е.
, т. е.
Иерархия ЕрпгоЕа дает более тонкую классификацию множеств из  . Доказана теорема: для любого
. Доказана теорема: для любого  существует непротиворечивая формула
существует непротиворечивая формула  , не имеющая Н. м.
, не имеющая Н. м. с предикатами из
с предикатами из  , то есть
, то есть  и
и  . В конструктивной безатомной булевой алгебре
. В конструктивной безатомной булевой алгебре  построен рекурсивно перечислимый идеал I (т. е. множество
построен рекурсивно перечислимый идеал I (т. е. множество  рекурсивно перечислимо) такой, что булева алгебра
рекурсивно перечислимо) такой, что булева алгебра  не конструктивизируема. Это позволило доказать нерекурсивную представимость решетки рекурсивно перечислимых множеств.
не конструктивизируема. Это позволило доказать нерекурсивную представимость решетки рекурсивно перечислимых множеств.
Исследование нумерованных линейных порядков позволило опровергнуть гипотезу сильной однородности для тьюринговых степеней.
Лит.:[1] Гончаров С. С, Дроботун Б. Н., "Сиб. матем. ж.", 1980, т. 21, [4] 2, с. 25-41; [2] Денисов С. Д., "Алгебра и логика", 1972, т. И, № 6, с. 648 - 55; [3] Дроботун Б. Н., "Сиб. матем. ж.", 1977, т. 18, №5, с. 1002-14; [4] Ершов Ю. Л., Теория нумераций, М., 1977; [5] Роджерс X., Теория рекурсивных функций и эффективная вычислимость, пер. с англ., М., 1972; [6] Feiner L., "J. Symbol. Logic", 1970, v. 35, p. 365-74; [7] eго же, там же, р. 375-77.
С. С. Гончаров

 , где
, где  - модель нек-рой фиксированной сигнатуры
- модель нек-рой фиксированной сигнатуры  и
и  - нумерация основного множества
- нумерация основного множества  модели
модели  Наиболее развитым направлением в изучении Н. м. является конструктивных моделей теория. Другим направлением в теории Н. м. является исследование проблемы сложности Н.. м., под к-рой понимается сложность множеств натуральных чисел
Наиболее развитым направлением в изучении Н. м. является конструктивных моделей теория. Другим направлением в теории Н. м. является исследование проблемы сложности Н.. м., под к-рой понимается сложность множеств натуральных чисел  либо множества
либо множества  . В качестве
. В качестве  здесь берется нек-рая гёделева нумерация всех формул сигнатуры
здесь берется нек-рая гёделева нумерация всех формул сигнатуры  где константы
где константы  не принадлежат сигнатуре
не принадлежат сигнатуре  - это множество всех замкнутых формул сигнатуры
- это множество всех замкнутых формул сигнатуры  истинных на системе
истинных на системе  , к-рая получается из системы
, к-рая получается из системы  обогащением сигнатуры
обогащением сигнатуры  до
до  , причем значение константы
, причем значение константы  полагает равным элементу
полагает равным элементу  означает соответственно, множество всех бескванторных предложений, истинных на системе
означает соответственно, множество всех бескванторных предложений, истинных на системе 
 и
и  обозначают соответственно арифметическую и аналитическую иерархии относительно множества А.
обозначают соответственно арифметическую и аналитическую иерархии относительно множества А. , то существует нумерация
, то существует нумерация 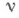 модели
модели  такая, что
такая, что  то есть
то есть  рекурсивно относительно множества
рекурсивно относительно множества  всех гёделевых номеров хтаких вычислимых относительно Афункций
всех гёделевых номеров хтаких вычислимых относительно Афункций  , для к-рых
, для к-рых  определено.
определено. , то существует нумерация
, то существует нумерация  модели
модели  такая, что
такая, что  то есть
то есть  есть гиперарифметич. множество относительно А; эти оценки сложности являются в нек-ром смысле точными.
есть гиперарифметич. множество относительно А; эти оценки сложности являются в нек-ром смысле точными. сложности
сложности  , т. е.
, т. е.
 . Доказана теорема: для любого
. Доказана теорема: для любого  существует непротиворечивая формула
существует непротиворечивая формула  , не имеющая Н. м.
, не имеющая Н. м. с предикатами из
с предикатами из  , то есть
, то есть  и
и  . В конструктивной безатомной булевой алгебре
. В конструктивной безатомной булевой алгебре  построен рекурсивно перечислимый идеал I (т. е. множество
построен рекурсивно перечислимый идеал I (т. е. множество  рекурсивно перечислимо) такой, что булева алгебра
рекурсивно перечислимо) такой, что булева алгебра  не конструктивизируема. Это позволило доказать нерекурсивную представимость решетки рекурсивно перечислимых множеств.
не конструктивизируема. Это позволило доказать нерекурсивную представимость решетки рекурсивно перечислимых множеств.