"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
НУМЕРАЦИЯ
Значение НУМЕРАЦИЯ в математической энциклопедии:
- основное понятие раздела теории алгоритмов - теории нумераций, изучающей общие свойства классов объектов, занумерованных с помощью каких-либо конструктивных объектов. В роли конструктивных объектов, служащих номерами элементов рассматриваемых классов, чаще всего выступают натуральные числа.
Идея Н. объектов нечисловой природы (напр., ло-гич. формул) натуральными числами и перенесение содержательных утверждений об этих объектах в область формальной арифметики натуральных чисел впервые были использованы К. Гёделем  при доказательстве Гёделя теоремы о неполноте арифметики Пеано. В дальнейшем эти идеи были использованы для Н. фундаментальных объектов теории алгоритмов таких, как Тьюринга машин, частично рекурсивных функций и рекурсивно перечислимых множеств. Наделение этих классов объектов подходящими Н. позволило во многих случаях выяснить более отчетливо природу этих объектов, выявить ряд их важных и новых свойств. Так возникла идея о систематич. изучении Н. произвольных множеств. При реализации этой идеи было замечено, что многие известные результаты теории алгоритмов оказываются следствиями общих закономерностей теории Н. (о построении теории Н., создании ее специфич. понятий и методов, о формировании перспективных направлений в теории Н. см. [1] - [4]). В частности, был плодотворно использован язык теории категорий, позволивший взглянуть на проблематику теории Н. с новой точки зрения (см. [4]).
при доказательстве Гёделя теоремы о неполноте арифметики Пеано. В дальнейшем эти идеи были использованы для Н. фундаментальных объектов теории алгоритмов таких, как Тьюринга машин, частично рекурсивных функций и рекурсивно перечислимых множеств. Наделение этих классов объектов подходящими Н. позволило во многих случаях выяснить более отчетливо природу этих объектов, выявить ряд их важных и новых свойств. Так возникла идея о систематич. изучении Н. произвольных множеств. При реализации этой идеи было замечено, что многие известные результаты теории алгоритмов оказываются следствиями общих закономерностей теории Н. (о построении теории Н., создании ее специфич. понятий и методов, о формировании перспективных направлений в теории Н. см. [1] - [4]). В частности, был плодотворно использован язык теории категорий, позволивший взглянуть на проблематику теории Н. с новой точки зрения (см. [4]).
Нумерованным множеством наз. пара  где А- нек-рое счетное множество, а
где А- нек-рое счетное множество, а 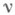 - некоторое отображение множества натуральных чисел
- некоторое отображение множества натуральных чисел  на А. Отображение
на А. Отображение  наз. нумерацией множества А. Если
наз. нумерацией множества А. Если  то пназ. номером объекта а при нумерации v. H.
то пназ. номером объекта а при нумерации v. H. множества Асводится к Н.
множества Асводится к Н.  множества А(отношение сводимости Н. обозначается
множества А(отношение сводимости Н. обозначается 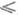 ), если существует с одноместная общерекурсивная функция f такая, что
), если существует с одноместная общерекурсивная функция f такая, что  для всех
для всех  . Нумерации
. Нумерации  и
и 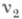 множества Аназ. эквивалентными, если
множества Аназ. эквивалентными, если  и
и  .С точки зрения теории Н. эквивалентные Н.
.С точки зрения теории Н. эквивалентные Н.
одного и того же множества неразличимы. По этой причине объектом исследования обычно является множество  - множество классов эквивалентных Н. множества А, частично упорядоченное отношением сводимости Н.
- множество классов эквивалентных Н. множества А, частично упорядоченное отношением сводимости Н. . Часто рассматривается и множество
. Часто рассматривается и множество  - множество классов эквивалентных Н. множества А, сводящихся к Н.
- множество классов эквивалентных Н. множества А, сводящихся к Н.  . Множества
. Множества  и
и  во многих случаях служат нек-рой "мерой сложности" множества А.
во многих случаях служат нек-рой "мерой сложности" множества А.
При сравнении Н. двух множеств Аи Восновным понятием является понятие морфизма. Морфизмом из нумерованного множества  в нумерованное множество
в нумерованное множество 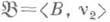 наз. всякое отображение
наз. всякое отображение 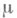 из Ав В, для к-рого существует одноместная общере-курсивная функция
из Ав В, для к-рого существует одноместная общере-курсивная функция  такая, что
такая, что  для всех
для всех  . Через
. Через  обозначают множество всевозможных морфизмов из
обозначают множество всевозможных морфизмов из  в
в  . С изучением множеств Мог, в частности с выяснением возможности наделения этого множества "хорошими" Н., тесно связаны многие вопросы общей теории алгоритмов.
. С изучением множеств Мог, в частности с выяснением возможности наделения этого множества "хорошими" Н., тесно связаны многие вопросы общей теории алгоритмов.
Категория  нумерованных множеств состоит из нумерованных множеств и морфизмов. Исследование свойств этой категории
нумерованных множеств состоит из нумерованных множеств и морфизмов. Исследование свойств этой категории  является основной задачей теории Н. Исходным пунктом такого исследования часто является изучение связей нумерованных множеств с важнейшими конкретными Н.- нумерацией Клнни
является основной задачей теории Н. Исходным пунктом такого исследования часто является изучение связей нумерованных множеств с важнейшими конкретными Н.- нумерацией Клнни  всех одноместных частично рекурсивных функций и нумераций Поста
всех одноместных частично рекурсивных функций и нумераций Поста  всех рекурсивно перечисли-мых множеств. В теории алгоритмов доказано существование двуместной частично рекурсивной функции
всех рекурсивно перечисли-мых множеств. В теории алгоритмов доказано существование двуместной частично рекурсивной функции  универсальной для класса всех одноместных частично рекурсивных функций, т. е. такой, что для любой частично рекурсивной функции f(х)можно найти число
универсальной для класса всех одноместных частично рекурсивных функций, т. е. такой, что для любой частично рекурсивной функции f(х)можно найти число  такое, что
такое, что 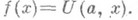 Нумерация Клини j задается тогда следующим образом:
Нумерация Клини j задается тогда следующим образом:  Если
Если  обозначает область значений функции
обозначает область значений функции  , то получаем нумерацию Поста
, то получаем нумерацию Поста  всех рекурсивно перечислимых множеств.
всех рекурсивно перечислимых множеств.
Фундаментальную роль при исследовании категории  играет введенное А. И. Мальцевым понятие полной Н., к-рое в самой общей форме синтезировало главные свойства нумераций Клини
играет введенное А. И. Мальцевым понятие полной Н., к-рое в самой общей форме синтезировало главные свойства нумераций Клини  и Поста
и Поста  . Н.
. Н. множества Аназ. полной, если среди элементов множества Аимеется такой выделенный элемент а, что для любой одноместной частично рекурсивной функции f существует одноместная общерекурсивная функция
множества Аназ. полной, если среди элементов множества Аимеется такой выделенный элемент а, что для любой одноместной частично рекурсивной функции f существует одноместная общерекурсивная функция  такая, что
такая, что

Полные Н. играют роль "инъективных" элементов категории  и наличие у Аполных Н. свидетельствует о значительной универсальности и важности класса объектов А.
и наличие у Аполных Н. свидетельствует о значительной универсальности и важности класса объектов А.
В частности, и нумерация Клини 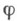 частично рекурсивных функций, и нумерация Поста
частично рекурсивных функций, и нумерация Поста  рекурсивно перечислимых множеств суть полные Н. (в первом случае выделенным элементом
рекурсивно перечислимых множеств суть полные Н. (в первом случае выделенным элементом  является нигде не определенная функция, а во втором - пустое множество). Важным направлением в исследовании категории
является нигде не определенная функция, а во втором - пустое множество). Важным направлением в исследовании категории  является также выделение и изучение различных видов подобъектов нумерованных множеств (см. [4]).
является также выделение и изучение различных видов подобъектов нумерованных множеств (см. [4]).
Часть теории Н., связанная с изучением нумераций Клини и Поста, а также их подобъектов, наиболее разработана, т. к. в этих случаях использование методов теории алгоритмов наиболее эффективно. Здесь в первую очередь изучаются т. н. вычислимые Н. Если множество А, напр., является семейством рекурсивно перечислимых множеств, то Н. этого семейства наз. вычислимой, если отношение
этого семейства наз. вычислимой, если отношение  само является рекурсивно перечислимым. Множество классов эквивалентных вычислимых Н. семейства Аобозначают
само является рекурсивно перечислимым. Множество классов эквивалентных вычислимых Н. семейства Аобозначают  . Это множество, как и
. Это множество, как и  , частично упорядочивается отношением сводимости Н.
, частично упорядочивается отношением сводимости Н.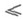 . Максимальный элемент множества
. Максимальный элемент множества  , если он существует, наз. главной вычислимой нумерацией семейства А. В частности, нумерации Клини и Поста являются главными вычислимыми Н. для соответствующих семейств Ф (всех одноместных частично рекурсивных функций) и Р(всех рекурсивно перечислимых множеств). Большое число работ в теории Н. посвящено изучению множеств
, если он существует, наз. главной вычислимой нумерацией семейства А. В частности, нумерации Клини и Поста являются главными вычислимыми Н. для соответствующих семейств Ф (всех одноместных частично рекурсивных функций) и Р(всех рекурсивно перечислимых множеств). Большое число работ в теории Н. посвящено изучению множеств 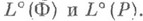 При этом нужно учесть, что многие свойства частично рекурсивных функций и рекурсивно перечислимых множеств, выявленные в теории алгоритмов, по существу являются отражениями алгебраич. свойств множеств
При этом нужно учесть, что многие свойства частично рекурсивных функций и рекурсивно перечислимых множеств, выявленные в теории алгоритмов, по существу являются отражениями алгебраич. свойств множеств  и
и  . Так, напр., легко укладываются в схему теории Н. изучаемые в теории алгоритмов и играющие там важную роль так наз. m-степени множеств. Если рассматривать семейство А, состоящее всего из двух множеств
. Так, напр., легко укладываются в схему теории Н. изучаемые в теории алгоритмов и играющие там важную роль так наз. m-степени множеств. Если рассматривать семейство А, состоящее всего из двух множеств  и
и  , то т- степени множеств есть не что иное, как L(A), а т- степени рекурсивно перечислимых множеств суть
, то т- степени множеств есть не что иное, как L(A), а т- степени рекурсивно перечислимых множеств суть 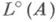 Имеется полное алгебраич. описание устройства множеств
Имеется полное алгебраич. описание устройства множеств  (см. [4]).
(см. [4]).
Пусть А- нек-рое семейство рекурсивно перечислимых множеств (для частично рекурсивных функций рассматриваемые понятия вводятся аналогично). Индексным (или номерным) множеством семейства Аназ. множество

номеров рекурсивно перечислимых множеств семейства Ав нумерации Поста. В теории Н. изучаются индексные множества  для различных семейств А. Так, теорема Раиса - Шапиро дает описание тех семейств А, для к-рых множество
для различных семейств А. Так, теорема Раиса - Шапиро дает описание тех семейств А, для к-рых множество  рекурсивно перечислимо. Такие семейства в теории Н. носят название вполне перечислимых классов. Даны также описания других видов подобъектов нумерации Поста - специальных стандартных классов, факторизации и ретрактов. Большую роль играют т. н. стандартные классы.
рекурсивно перечислимо. Такие семейства в теории Н. носят название вполне перечислимых классов. Даны также описания других видов подобъектов нумерации Поста - специальных стандартных классов, факторизации и ретрактов. Большую роль играют т. н. стандартные классы.
Семейство  рекурсивно перечислимых множеств наз. стандартным классом, если существует общерекурсивная функция
рекурсивно перечислимых множеств наз. стандартным классом, если существует общерекурсивная функция  такая, что:
такая, что:
 при этом, если
при этом, если  Стандартные классы тесно связаны с полными Н. В настоящее время (1982) нет удовлетворительного описания стандартных классов. Такое описание могло бы пролить свет на многие вопросы теории алгоритмов. В теории Н. также рассматривались главные, эффективно-главные и другие виды подобъектов нумерации Поста (см. [4]).
Стандартные классы тесно связаны с полными Н. В настоящее время (1982) нет удовлетворительного описания стандартных классов. Такое описание могло бы пролить свет на многие вопросы теории алгоритмов. В теории Н. также рассматривались главные, эффективно-главные и другие виды подобъектов нумерации Поста (см. [4]).
Алгоритмич. аналогом понятия алгебраической системы, т. е. множества с заданными на нем функциями и предикатами, является понятие нумерованной, или конструктивной, алгебраической системы. Идея состоит в следующем. Рассматриваемое множество Анаделяется Н. Вместо функций и предикатов, заданных на объектах множества А, рассматриваются "переводы" этих функций и предикатов, оперирующие соответствующим образом с натуральными числами как с номерами объектов множества А. Если при этом можно добиться того, чтобы эти "переводы" функций и предикатов были общерекурсивными, то говорят, что данная алгебраич. система конструктивизируема. Первое систематич. изучение теории конструктивных алгебраич. систем было предпринято А. И. Мальцевым [3].
Следует отметить два наиболее ярких применения теории Н. к задачам теории алгоритмов: завершение построения теории Майхилла об универсальных объектах и построение теории вычислимых функционалов конечных типов (см. [4]). Методы и результаты теории Н. могут быть использованы в смежных к математич. логике и теории алгоритмов науках, в частности в программировании. Так, с помощью теории Н. могут быть решены нек-рые вопросы семантики языков программирования.
Лит.:[1] Мальцев А. И., Алгоритмы и рекурсивные функции, М., 1965; [2] его же, "Успехи матем. наук", 1961, т. 16, в. 3, с. 3-60; [3] Успенский В. А.. Лекции о вычислимых функциях, М., 1960; [4] Ершов Ю. Л., Теория нумераций, М., 1977.

 при доказательстве Гёделя теоремы о неполноте арифметики Пеано. В дальнейшем эти идеи были использованы для Н. фундаментальных объектов теории алгоритмов таких, как Тьюринга машин, частично рекурсивных функций и рекурсивно перечислимых множеств. Наделение этих классов объектов подходящими Н. позволило во многих случаях выяснить более отчетливо природу этих объектов, выявить ряд их важных и новых свойств. Так возникла идея о систематич. изучении Н. произвольных множеств. При реализации этой идеи было замечено, что многие известные результаты теории алгоритмов оказываются следствиями общих закономерностей теории Н. (о построении теории Н., создании ее специфич. понятий и методов, о формировании перспективных направлений в теории Н. см. [1] - [4]). В частности, был плодотворно использован язык теории категорий, позволивший взглянуть на проблематику теории Н. с новой точки зрения (см. [4]).
при доказательстве Гёделя теоремы о неполноте арифметики Пеано. В дальнейшем эти идеи были использованы для Н. фундаментальных объектов теории алгоритмов таких, как Тьюринга машин, частично рекурсивных функций и рекурсивно перечислимых множеств. Наделение этих классов объектов подходящими Н. позволило во многих случаях выяснить более отчетливо природу этих объектов, выявить ряд их важных и новых свойств. Так возникла идея о систематич. изучении Н. произвольных множеств. При реализации этой идеи было замечено, что многие известные результаты теории алгоритмов оказываются следствиями общих закономерностей теории Н. (о построении теории Н., создании ее специфич. понятий и методов, о формировании перспективных направлений в теории Н. см. [1] - [4]). В частности, был плодотворно использован язык теории категорий, позволивший взглянуть на проблематику теории Н. с новой точки зрения (см. [4]). где А- нек-рое счетное множество, а
где А- нек-рое счетное множество, а 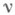 - некоторое отображение множества натуральных чисел
- некоторое отображение множества натуральных чисел  на А. Отображение
на А. Отображение  наз. нумерацией множества А. Если
наз. нумерацией множества А. Если  то пназ. номером объекта а при нумерации v. H.
то пназ. номером объекта а при нумерации v. H. множества Асводится к Н.
множества Асводится к Н.  множества А(отношение сводимости Н. обозначается
множества А(отношение сводимости Н. обозначается 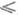 ), если существует с одноместная общерекурсивная функция f такая, что
), если существует с одноместная общерекурсивная функция f такая, что  для всех
для всех  . Нумерации
. Нумерации  и
и 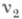 множества Аназ. эквивалентными, если
множества Аназ. эквивалентными, если  и
и  .С точки зрения теории Н. эквивалентные Н.
.С точки зрения теории Н. эквивалентные Н. - множество классов эквивалентных Н. множества А, частично упорядоченное отношением сводимости Н.
- множество классов эквивалентных Н. множества А, частично упорядоченное отношением сводимости Н. . Часто рассматривается и множество
. Часто рассматривается и множество  - множество классов эквивалентных Н. множества А, сводящихся к Н.
- множество классов эквивалентных Н. множества А, сводящихся к Н.  . Множества
. Множества  и
и  во многих случаях служат нек-рой "мерой сложности" множества А.
во многих случаях служат нек-рой "мерой сложности" множества А. в нумерованное множество
в нумерованное множество 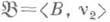 наз. всякое отображение
наз. всякое отображение 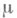 из Ав В, для к-рого существует одноместная общере-курсивная функция
из Ав В, для к-рого существует одноместная общере-курсивная функция  такая, что
такая, что  для всех
для всех  . Через
. Через  обозначают множество всевозможных морфизмов из
обозначают множество всевозможных морфизмов из  в
в  . С изучением множеств Мог, в частности с выяснением возможности наделения этого множества "хорошими" Н., тесно связаны многие вопросы общей теории алгоритмов.
. С изучением множеств Мог, в частности с выяснением возможности наделения этого множества "хорошими" Н., тесно связаны многие вопросы общей теории алгоритмов. нумерованных множеств состоит из нумерованных множеств и морфизмов. Исследование свойств этой категории
нумерованных множеств состоит из нумерованных множеств и морфизмов. Исследование свойств этой категории  является основной задачей теории Н. Исходным пунктом такого исследования часто является изучение связей нумерованных множеств с важнейшими конкретными Н.- нумерацией Клнни
является основной задачей теории Н. Исходным пунктом такого исследования часто является изучение связей нумерованных множеств с важнейшими конкретными Н.- нумерацией Клнни  всех одноместных частично рекурсивных функций и нумераций Поста
всех одноместных частично рекурсивных функций и нумераций Поста  всех рекурсивно перечисли-мых множеств. В теории алгоритмов доказано существование двуместной частично рекурсивной функции
всех рекурсивно перечисли-мых множеств. В теории алгоритмов доказано существование двуместной частично рекурсивной функции  универсальной для класса всех одноместных частично рекурсивных функций, т. е. такой, что для любой частично рекурсивной функции f(х)можно найти число
универсальной для класса всех одноместных частично рекурсивных функций, т. е. такой, что для любой частично рекурсивной функции f(х)можно найти число  такое, что
такое, что 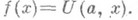 Нумерация Клини j задается тогда следующим образом:
Нумерация Клини j задается тогда следующим образом:  Если
Если  обозначает область значений функции
обозначает область значений функции  , то получаем нумерацию Поста
, то получаем нумерацию Поста  всех рекурсивно перечислимых множеств.
всех рекурсивно перечислимых множеств. играет введенное А. И. Мальцевым понятие полной Н., к-рое в самой общей форме синтезировало главные свойства нумераций Клини
играет введенное А. И. Мальцевым понятие полной Н., к-рое в самой общей форме синтезировало главные свойства нумераций Клини  и Поста
и Поста  . Н.
. Н. множества Аназ. полной, если среди элементов множества Аимеется такой выделенный элемент а, что для любой одноместной частично рекурсивной функции f существует одноместная общерекурсивная функция
множества Аназ. полной, если среди элементов множества Аимеется такой выделенный элемент а, что для любой одноместной частично рекурсивной функции f существует одноместная общерекурсивная функция  такая, что
такая, что
 и наличие у Аполных Н. свидетельствует о значительной универсальности и важности класса объектов А.
и наличие у Аполных Н. свидетельствует о значительной универсальности и важности класса объектов А. частично рекурсивных функций, и нумерация Поста
частично рекурсивных функций, и нумерация Поста  рекурсивно перечислимых множеств суть полные Н. (в первом случае выделенным элементом
рекурсивно перечислимых множеств суть полные Н. (в первом случае выделенным элементом  является нигде не определенная функция, а во втором - пустое множество). Важным направлением в исследовании категории
является нигде не определенная функция, а во втором - пустое множество). Важным направлением в исследовании категории  является также выделение и изучение различных видов подобъектов нумерованных множеств (см. [4]).
является также выделение и изучение различных видов подобъектов нумерованных множеств (см. [4]). этого семейства наз. вычислимой, если отношение
этого семейства наз. вычислимой, если отношение  само является рекурсивно перечислимым. Множество классов эквивалентных вычислимых Н. семейства Аобозначают
само является рекурсивно перечислимым. Множество классов эквивалентных вычислимых Н. семейства Аобозначают  . Это множество, как и
. Это множество, как и  , частично упорядочивается отношением сводимости Н.
, частично упорядочивается отношением сводимости Н. . Максимальный элемент множества
. Максимальный элемент множества  , если он существует, наз. главной вычислимой нумерацией семейства А. В частности, нумерации Клини и Поста являются главными вычислимыми Н. для соответствующих семейств Ф (всех одноместных частично рекурсивных функций) и Р(всех рекурсивно перечислимых множеств). Большое число работ в теории Н. посвящено изучению множеств
, если он существует, наз. главной вычислимой нумерацией семейства А. В частности, нумерации Клини и Поста являются главными вычислимыми Н. для соответствующих семейств Ф (всех одноместных частично рекурсивных функций) и Р(всех рекурсивно перечислимых множеств). Большое число работ в теории Н. посвящено изучению множеств 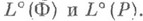 При этом нужно учесть, что многие свойства частично рекурсивных функций и рекурсивно перечислимых множеств, выявленные в теории алгоритмов, по существу являются отражениями алгебраич. свойств множеств
При этом нужно учесть, что многие свойства частично рекурсивных функций и рекурсивно перечислимых множеств, выявленные в теории алгоритмов, по существу являются отражениями алгебраич. свойств множеств  и
и  . Так, напр., легко укладываются в схему теории Н. изучаемые в теории алгоритмов и играющие там важную роль так наз. m-степени множеств. Если рассматривать семейство А, состоящее всего из двух множеств
. Так, напр., легко укладываются в схему теории Н. изучаемые в теории алгоритмов и играющие там важную роль так наз. m-степени множеств. Если рассматривать семейство А, состоящее всего из двух множеств  и
и  , то т- степени множеств есть не что иное, как L(A), а т- степени рекурсивно перечислимых множеств суть
, то т- степени множеств есть не что иное, как L(A), а т- степени рекурсивно перечислимых множеств суть 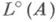 Имеется полное алгебраич. описание устройства множеств
Имеется полное алгебраич. описание устройства множеств  (см. [4]).
(см. [4]).
 для различных семейств А. Так, теорема Раиса - Шапиро дает описание тех семейств А, для к-рых множество
для различных семейств А. Так, теорема Раиса - Шапиро дает описание тех семейств А, для к-рых множество  рекурсивно перечислимо. Такие семейства в теории Н. носят название вполне перечислимых классов. Даны также описания других видов подобъектов нумерации Поста - специальных стандартных классов, факторизации и ретрактов. Большую роль играют т. н. стандартные классы.
рекурсивно перечислимо. Такие семейства в теории Н. носят название вполне перечислимых классов. Даны также описания других видов подобъектов нумерации Поста - специальных стандартных классов, факторизации и ретрактов. Большую роль играют т. н. стандартные классы. рекурсивно перечислимых множеств наз. стандартным классом, если существует общерекурсивная функция
рекурсивно перечислимых множеств наз. стандартным классом, если существует общерекурсивная функция  такая, что:
такая, что:
 при этом, если
при этом, если  Стандартные классы тесно связаны с полными Н. В настоящее время (1982) нет удовлетворительного описания стандартных классов. Такое описание могло бы пролить свет на многие вопросы теории алгоритмов. В теории Н. также рассматривались главные, эффективно-главные и другие виды подобъектов нумерации Поста (см. [4]).
Стандартные классы тесно связаны с полными Н. В настоящее время (1982) нет удовлетворительного описания стандартных классов. Такое описание могло бы пролить свет на многие вопросы теории алгоритмов. В теории Н. также рассматривались главные, эффективно-главные и другие виды подобъектов нумерации Поста (см. [4]).