"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
НУЛЬМЕРНОЕ ОТОБРАЖЕНИЕЗначение НУЛЬМЕРНОЕ ОТОБРАЖЕНИЕ в математической энциклопедии:
- непрерывное отображение  ( ( - топологич. пространства) такое, что - топологич. пространства) такое, что  - нульмерное множество (в смысле ind) для всякого - нульмерное множество (в смысле ind) для всякого 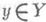 . Применение Н. о. и близких к ним позволяет свести исследование данного пространства к изучению другого, более простого. Так, многие размерностные свойства и другие кардинальнозначные инварианты переходят от Xк Y(или, чаще, от Y к X). . Применение Н. о. и близких к ним позволяет свести исследование данного пространства к изучению другого, более простого. Так, многие размерностные свойства и другие кардинальнозначные инварианты переходят от Xк Y(или, чаще, от Y к X). Пример). Всякое метрич. пространство Xс  допускает вполне Н. о. в пространство Yсо счетной базой, причем допускает вполне Н. о. в пространство Yсо счетной базой, причем  (теорема Катетова). При этом полная нульмерность означает, что для любого (теорема Катетова). При этом полная нульмерность означает, что для любого  и любого и любого  существует окрестность существует окрестность  , прообраз , прообраз  к-рой распадается в дискретную в Xсистему открытых в Xмножеств диаметра < к-рой распадается в дискретную в Xсистему открытых в Xмножеств диаметра < Пример 2. Если Н. о.  где X- нормальное локально связное пространство, является совершенным отображением, то вес X совпадает с весом Y. где X- нормальное локально связное пространство, является совершенным отображением, то вес X совпадает с весом Y. Лит.:[1] Александров П. С, Пасынков Б. А., Введение в теорию размерности, М., 1973. М. И. Войцеховский.
|

 (
( - топологич. пространства) такое, что
- топологич. пространства) такое, что  - нульмерное множество (в смысле ind) для всякого
- нульмерное множество (в смысле ind) для всякого 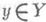 . Применение Н. о. и близких к ним позволяет свести исследование данного пространства к изучению другого, более простого. Так, многие размерностные свойства и другие кардинальнозначные инварианты переходят от Xк Y(или, чаще, от Y к X).
. Применение Н. о. и близких к ним позволяет свести исследование данного пространства к изучению другого, более простого. Так, многие размерностные свойства и другие кардинальнозначные инварианты переходят от Xк Y(или, чаще, от Y к X). допускает вполне Н. о. в пространство Yсо счетной базой, причем
допускает вполне Н. о. в пространство Yсо счетной базой, причем  (теорема Катетова). При этом полная нульмерность означает, что для любого
(теорема Катетова). При этом полная нульмерность означает, что для любого  и любого
и любого  существует окрестность
существует окрестность  , прообраз
, прообраз  к-рой распадается в дискретную в Xсистему открытых в Xмножеств диаметра <
к-рой распадается в дискретную в Xсистему открытых в Xмножеств диаметра <
 где X- нормальное локально связное пространство, является совершенным отображением, то вес X совпадает с весом Y.
где X- нормальное локально связное пространство, является совершенным отображением, то вес X совпадает с весом Y.