"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
НОРМИРОВАНИЕ
Значение НОРМИРОВАНИЕ в математической энциклопедии:
логарифмическое нормирование, оценка поля,- отображение  поля Кв
поля Кв  где Г - линейно упорядоченная абелева группа, а присоединяемый элемент
где Г - линейно упорядоченная абелева группа, а присоединяемый элемент  считается больше любого элемента из группы
считается больше любого элемента из группы  и
и  для любого
для любого  . При этом Н. должно удовлетворять следующим условиям:
. При этом Н. должно удовлетворять следующим условиям:

Образ  при отображении vявляется подгруппой группы Г и называется группой значений нормирования v. Всюду в дальнейшем будет предполагаться, что
при отображении vявляется подгруппой группы Г и называется группой значений нормирования v. Всюду в дальнейшем будет предполагаться, что  совпадает с Г.
совпадает с Г.
Теми же аксиомами определяется логарифм и-ческое нормирование колец. Всякое кольцо с неархимедовым абсолютным значением может быть превращено в логарифмически нормированное кольцо, если в группоиде значений перейти от мультипликативной записи к аддитивной и заменить упорядоченность на инверсную. Элемент 0 при этом естественно обозначить символом  . Обратный переход от кольца с логарифмическим Н. к кольцу с неархимедовым абсолютным значением также возможен. Если в кольце было задано неархимедово вещественное нормирование, то соответствующий переход можно получить, заменяя любое положительное действительное число
. Обратный переход от кольца с логарифмическим Н. к кольцу с неархимедовым абсолютным значением также возможен. Если в кольце было задано неархимедово вещественное нормирование, то соответствующий переход можно получить, заменяя любое положительное действительное число  числом
числом  . Получающееся при этом логарифмическое Н. также принято называть вещественным.
. Получающееся при этом логарифмическое Н. также принято называть вещественным.
Нормирования  наз. эквивалентными, если существует такой изоморфизм
наз. эквивалентными, если существует такой изоморфизм  упорядоченных групп, что для всех ненулевых элементов
упорядоченных групп, что для всех ненулевых элементов 

Множество таких элементов хполя К, что  , является подкольцом Аполя Ки наз. кольцом нормирования ев поле К. Кольцо Н. всегда является локальным кольцом. Элементы поля К, для которых
, является подкольцом Аполя Ки наз. кольцом нормирования ев поле К. Кольцо Н. всегда является локальным кольцом. Элементы поля К, для которых  образуют максимальный идеал
образуют максимальный идеал  кольца А; он наз. идеалом нормирования v. Факторкольцо
кольца А; он наз. идеалом нормирования v. Факторкольцо  , являющееся полем, наз. полем вычетов нормирования
, являющееся полем, наз. полем вычетов нормирования  .
.
Пусть в поле Кзаданы Н.  и
и  . Кольца этих Н., рассматриваемые как подкольца поля К, тогда и только тогда совпадают, когда эти Н. эквивалентны. Таким образом, обозрение всех (с точностью до эквивалентности) Н. поля Ксводится к обозрению всех таких подколец, которые могут служить для этого поля кольцами Н. Описание таких подколец дает следующая теорема: подкольцо Аполя Ктогда и только тогда может служить для этого поля кольцом Н., когда для всякого ненулевого элемента
. Кольца этих Н., рассматриваемые как подкольца поля К, тогда и только тогда совпадают, когда эти Н. эквивалентны. Таким образом, обозрение всех (с точностью до эквивалентности) Н. поля Ксводится к обозрению всех таких подколец, которые могут служить для этого поля кольцами Н. Описание таких подколец дает следующая теорема: подкольцо Аполя Ктогда и только тогда может служить для этого поля кольцом Н., когда для всякого ненулевого элемента  , хотя бы один из элементов
, хотя бы один из элементов  принадлежит к А. Кольцо Н., таким образом, может быть абстрактно определено как целостное кольцо (область целостности), удовлетворяющее условию сформулированной выше теоремы по отношению к своему полю частных. Всякое такое кольцо служит кольцом т. н. канонического нормирования для своего поля частных, группой значений канонического Н. является группа
принадлежит к А. Кольцо Н., таким образом, может быть абстрактно определено как целостное кольцо (область целостности), удовлетворяющее условию сформулированной выше теоремы по отношению к своему полю частных. Всякое такое кольцо служит кольцом т. н. канонического нормирования для своего поля частных, группой значений канонического Н. является группа  , где U-мультипликативная группа обратимых элементов кольца А, упорядоченная отношением делимости.
, где U-мультипликативная группа обратимых элементов кольца А, упорядоченная отношением делимости.
Кольца Н. можно определить еще одним способом. Если  - два локальных кольца с максимальными идеалами ти п соответственно, то говорят, что Вдоминирует А, если
- два локальных кольца с максимальными идеалами ти п соответственно, то говорят, что Вдоминирует А, если  . Отношение доминирования является отношением частичного порядка на множестве подколец поля К. Максимальные элементы этого множества и только они являются кольцами Н. поля К. Если А- кольцо Н., а
. Отношение доминирования является отношением частичного порядка на множестве подколец поля К. Максимальные элементы этого множества и только они являются кольцами Н. поля К. Если А- кольцо Н., а  - кольцо с тем же полем частных, что и А, то В также кольцо Н. и Вявляется локализацией кольца Апо нек-рому простому идеалу.
- кольцо с тем же полем частных, что и А, то В также кольцо Н. и Вявляется локализацией кольца Апо нек-рому простому идеалу.
Примеры нормирований. 1) Нормирование поля, определяемое формулой:

наз. несобственным, или тривиальным, Н. Таково любое Н. конечного поля. Ему соответствует точка  (тождественное отображение К).
(тождественное отображение К).
2) Пусть k - нек-рое поле и  - поле формальных степенных рядов над k. Сопоставление ряду
- поле формальных степенных рядов над k. Сопоставление ряду  его порядка п(а нулевому ряду
его порядка п(а нулевому ряду  ) продолжается до Н. с группой значений
) продолжается до Н. с группой значений  (аддитивная группа целых чисел) и кольцом Н.
(аддитивная группа целых чисел) и кольцом Н.  . Ассоциированная точка сопоставляет ряду
. Ассоциированная точка сопоставляет ряду  свободный член
свободный член  .
.
Н. со значениями в группе  наз. дискретным; о их кольцах Н. см. Дискретного нормирования кольцо. Описание всех Н. поля рациональных чисел см. в [4].
наз. дискретным; о их кольцах Н. см. Дискретного нормирования кольцо. Описание всех Н. поля рациональных чисел см. в [4].
Для любой линейно упорядоченной абелевой группы Г существует Н. некоторого поля, группа значений к-рого изоморфна Г.
Идеалы колец нормирования. Множество идеалов кольца Н. линейно упорядочено относительно включения, любой идеал конечного типа- главный, т. е. кольцо Н. является Везу кольцом. Более полно описание строения идеалов кольца Н. можно дать в терминах группы значений Н.
Подмножество Млинейно упорядоченного множества наз. мажорным (или м. <ажором), если из соотношений  и
и  следует, что
следует, что  . Пусть А- кольцо Н. vполя Кс группой значений
. Пусть А- кольцо Н. vполя Кс группой значений  - подполугруппа положительных элементов Г и М- мажорное множество в
- подполугруппа положительных элементов Г и М- мажорное множество в  . Отображение
. Отображение 
 является биективным (взаимно однозначным) отображением множества мажорных подмножеств из
является биективным (взаимно однозначным) отображением множества мажорных подмножеств из  на множество идеалов кольца А. При этом главным идеалам соответствуют мажоры, обладающие минимальным элементом. Простым идеалам тоже соответствуют мажоры специального вида, а именно: мажоры вида
на множество идеалов кольца А. При этом главным идеалам соответствуют мажоры, обладающие минимальным элементом. Простым идеалам тоже соответствуют мажоры специального вида, а именно: мажоры вида  где
где  - положительная часть нек-рой выпуклой подгруппы Нгруппы Г. Таким образом, устанавливается взаимно однозначное соответствие между простыми идеалами А и выпуклыми подгруппами группы значений Г.
- положительная часть нек-рой выпуклой подгруппы Нгруппы Г. Таким образом, устанавливается взаимно однозначное соответствие между простыми идеалами А и выпуклыми подгруппами группы значений Г.
Пусть р- простой идеал, соответствующий выпуклой подгруппе H, тогда композиция отображений  будет Н. поля Кс кольцом Н.
будет Н. поля Кс кольцом Н. 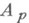 и идеалом Н. рА р ;кроме того, на поле
и идеалом Н. рА р ;кроме того, на поле  индуцируется Н. со значениями в группе Ни кольцом Н.
индуцируется Н. со значениями в группе Ни кольцом Н.  . Тем самым Н. расщепляется на более простые. Пусть А- кольцо Н., тогда простой спектр Абез нуля (Spec А-(0)) является линейно упорядоченным множеством и его тип наз. высотой, или рангом, соответствующего Н. Если Spec Аконечен, то высота Н. есть число элементов в Spec А-(0), и это число совпадает с числом выпуклых подгрупп группы Г, отличных от самой Г. Н. конечного ранга сводятся к Н. ранга 1. Последние характеризуются тем, что их группа значений - архимедова группа, т. е. изоморфна нек-рой подгруппе аддитивной группы
. Тем самым Н. расщепляется на более простые. Пусть А- кольцо Н., тогда простой спектр Абез нуля (Spec А-(0)) является линейно упорядоченным множеством и его тип наз. высотой, или рангом, соответствующего Н. Если Spec Аконечен, то высота Н. есть число элементов в Spec А-(0), и это число совпадает с числом выпуклых подгрупп группы Г, отличных от самой Г. Н. конечного ранга сводятся к Н. ранга 1. Последние характеризуются тем, что их группа значений - архимедова группа, т. е. изоморфна нек-рой подгруппе аддитивной группы  действительных чисел. В этом случае отображение
действительных чисел. В этом случае отображение  является ультраметрическим абсолютным значением поля К,
является ультраметрическим абсолютным значением поля К,
Важное свойство колец Н.- целозамкнутость. Более того, для произвольного целостного кольца Аего целое замыкание равно пересечению всех колец Н., содержащих А. Кольцо Н. вполне целозамкнуто тогда и только тогда, когда его Н. вещественное, т. е. имеет ранг 1. Кольцо Н. нётерово тогда и только тогда, когда Н. дискретно.
Связь нормирования и топологии. Пусть  Н. поля Kи
Н. поля Kи 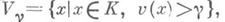 где
где  Совокупность всех
Совокупность всех  , образует фундаментальную систему окрестностей нуля топологии
, образует фундаментальную систему окрестностей нуля топологии  поля К, называемой топологией, определяемо й нормированием V. Топология
поля К, называемой топологией, определяемо й нормированием V. Топология  отделима и несвязна. Топология, индуцируемая
отделима и несвязна. Топология, индуцируемая  на кольце А, как правило, отлична от топологии локального кольца. Для нетривиального Н. поля Ктопология
на кольце А, как правило, отлична от топологии локального кольца. Для нетривиального Н. поля Ктопология  локально компактна тогда и только тогда, когда Н. vдискретно, кольцо Н. полное, а поле вычетов Н. vконечно; кольцо Апри этом будет компактно. Пополнение
локально компактна тогда и только тогда, когда Н. vдискретно, кольцо Н. полное, а поле вычетов Н. vконечно; кольцо Апри этом будет компактно. Пополнение  поля Котносительно топологии
поля Котносительно топологии  является полем; Н. vпродолжается по непрерывности до Н.
является полем; Н. vпродолжается по непрерывности до Н. и топология
и топология  совпадает с
совпадает с  . Кольцо
. Кольцо  нормирования vявляется пополнением кольца Анормирования v.
нормирования vявляется пополнением кольца Анормирования v.
Нормирования  и
и  поля Кназ. независимым и, если топологии
поля Кназ. независимым и, если топологии  и
и  различны; это эквивалентно тому, что кольца нормирований
различны; это эквивалентно тому, что кольца нормирований  и .
и . порождают поле К. Неэквивалентные нормирования высоты 1 всегда независимы. Имеет место теорема аппроксимации для нормирований: пусть
порождают поле К. Неэквивалентные нормирования высоты 1 всегда независимы. Имеет место теорема аппроксимации для нормирований: пусть  - независимые нормирования,
- независимые нормирования,  тогда найдется такой элемент хполя К, что
тогда найдется такой элемент хполя К, что 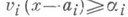 для всех
для всех  .
.
Продолжения нормирований. Если  - Н. поля L, а К- подполе L, то ограничение
- Н. поля L, а К- подполе L, то ограничение  нормирования
нормирования  на поле Кявляется Н. поля К, а его группа значений Г - подгруппой группы
на поле Кявляется Н. поля К, а его группа значений Г - подгруппой группы  наз. при этом продолжением Н. v. Обратно, если v- Н., a L расширение поля К, то всегда существует Н. поля L, продолжающее v. Индекс
наз. при этом продолжением Н. v. Обратно, если v- Н., a L расширение поля К, то всегда существует Н. поля L, продолжающее v. Индекс  подгруппы Г в группе
подгруппы Г в группе  наз. индексом ветвления Н.
наз. индексом ветвления Н.  относительно vи обозначается
относительно vи обозначается  Поле вычетов
Поле вычетов  нормирования vотождествляется с подполем поля вычетов
нормирования vотождествляется с подполем поля вычетов  степень расширения
степень расширения  обозначается
обозначается  и наз. степенью вычетов Н.
и наз. степенью вычетов Н.  относительно v. Продолжение
относительно v. Продолжение  нормирования vназ. непосредственным, если
нормирования vназ. непосредственным, если 
Пусть L - расширение поля  - множество всех продолжений Н. v на L. Если L - конечное расширение поля Кстепени п, то множество всех продолжений vконечно, и
- множество всех продолжений Н. v на L. Если L - конечное расширение поля Кстепени п, то множество всех продолжений vконечно, и

В ряде случаев это неравенство можно заменить на равенство, напр, когда  дискретно и либо Кполно, либо Lсепарабельно над К. Если L- нормальное расширение К, то продолжения
дискретно и либо Кполно, либо Lсепарабельно над К. Если L- нормальное расширение К, то продолжения  на Lпереводятся друг в друга K-автоморфизмами L, в частности если L- радикальное расширение К, то
на Lпереводятся друг в друга K-автоморфизмами L, в частности если L- радикальное расширение К, то  имеет единственное продолжение. В случае произвольного бесконечного расширения
имеет единственное продолжение. В случае произвольного бесконечного расширения  или продолжения
или продолжения  нормирования vстепень трансцендентности Lнад Кбольше или равна сумме
нормирования vстепень трансцендентности Lнад Кбольше или равна сумме  где
где  - степень трансцендентности расширения поля вычетов
- степень трансцендентности расширения поля вычетов  над полем вычетов
над полем вычетов  - размерность пространства
- размерность пространства 
Понятие "Н." ввел и изучил В. Крулль [1]. Это понятие широко используется также в алгебраич. геометрии. Так, в терминах "колец Н." строится абстрактная риманова поверхность поля (см. [3]).
Лит.:[1] Krull W., "J. reine und angew. Math.", 1932, Bd 167, S. 160-96; [2] Бурбаки Н., Коммутативная алгебра, пер. с франц., М., 1971; [3]3арисский О., Самюэль П., Коммутативная алгебра, пер. с англ., т. 2, М., 1963; [4] Курош А. Г., Лекции по общей алгебре, 2 изд., М., 1973.
В. И. Данилов.

 поля Кв
поля Кв  где Г - линейно упорядоченная абелева группа, а присоединяемый элемент
где Г - линейно упорядоченная абелева группа, а присоединяемый элемент  считается больше любого элемента из группы
считается больше любого элемента из группы  и
и  для любого
для любого  . При этом Н. должно удовлетворять следующим условиям:
. При этом Н. должно удовлетворять следующим условиям:
 при отображении vявляется подгруппой группы Г и называется группой значений нормирования v. Всюду в дальнейшем будет предполагаться, что
при отображении vявляется подгруппой группы Г и называется группой значений нормирования v. Всюду в дальнейшем будет предполагаться, что  совпадает с Г.
совпадает с Г. . Обратный переход от кольца с логарифмическим Н. к кольцу с неархимедовым абсолютным значением также возможен. Если в кольце было задано неархимедово вещественное нормирование, то соответствующий переход можно получить, заменяя любое положительное действительное число
. Обратный переход от кольца с логарифмическим Н. к кольцу с неархимедовым абсолютным значением также возможен. Если в кольце было задано неархимедово вещественное нормирование, то соответствующий переход можно получить, заменяя любое положительное действительное число  числом
числом  . Получающееся при этом логарифмическое Н. также принято называть вещественным.
. Получающееся при этом логарифмическое Н. также принято называть вещественным. наз. эквивалентными, если существует такой изоморфизм
наз. эквивалентными, если существует такой изоморфизм  упорядоченных групп, что для всех ненулевых элементов
упорядоченных групп, что для всех ненулевых элементов 

 , является подкольцом Аполя Ки наз. кольцом нормирования ев поле К. Кольцо Н. всегда является локальным кольцом. Элементы поля К, для которых
, является подкольцом Аполя Ки наз. кольцом нормирования ев поле К. Кольцо Н. всегда является локальным кольцом. Элементы поля К, для которых  образуют максимальный идеал
образуют максимальный идеал  кольца А; он наз. идеалом нормирования v. Факторкольцо
кольца А; он наз. идеалом нормирования v. Факторкольцо  , являющееся полем, наз. полем вычетов нормирования
, являющееся полем, наз. полем вычетов нормирования  .
. и
и  . Кольца этих Н., рассматриваемые как подкольца поля К, тогда и только тогда совпадают, когда эти Н. эквивалентны. Таким образом, обозрение всех (с точностью до эквивалентности) Н. поля Ксводится к обозрению всех таких подколец, которые могут служить для этого поля кольцами Н. Описание таких подколец дает следующая теорема: подкольцо Аполя Ктогда и только тогда может служить для этого поля кольцом Н., когда для всякого ненулевого элемента
. Кольца этих Н., рассматриваемые как подкольца поля К, тогда и только тогда совпадают, когда эти Н. эквивалентны. Таким образом, обозрение всех (с точностью до эквивалентности) Н. поля Ксводится к обозрению всех таких подколец, которые могут служить для этого поля кольцами Н. Описание таких подколец дает следующая теорема: подкольцо Аполя Ктогда и только тогда может служить для этого поля кольцом Н., когда для всякого ненулевого элемента  , хотя бы один из элементов
, хотя бы один из элементов  принадлежит к А. Кольцо Н., таким образом, может быть абстрактно определено как целостное кольцо (область целостности), удовлетворяющее условию сформулированной выше теоремы по отношению к своему полю частных. Всякое такое кольцо служит кольцом т. н. канонического нормирования для своего поля частных, группой значений канонического Н. является группа
принадлежит к А. Кольцо Н., таким образом, может быть абстрактно определено как целостное кольцо (область целостности), удовлетворяющее условию сформулированной выше теоремы по отношению к своему полю частных. Всякое такое кольцо служит кольцом т. н. канонического нормирования для своего поля частных, группой значений канонического Н. является группа  , где U-мультипликативная группа обратимых элементов кольца А, упорядоченная отношением делимости.
, где U-мультипликативная группа обратимых элементов кольца А, упорядоченная отношением делимости. - два локальных кольца с максимальными идеалами ти п соответственно, то говорят, что Вдоминирует А, если
- два локальных кольца с максимальными идеалами ти п соответственно, то говорят, что Вдоминирует А, если  . Отношение доминирования является отношением частичного порядка на множестве подколец поля К. Максимальные элементы этого множества и только они являются кольцами Н. поля К. Если А- кольцо Н., а
. Отношение доминирования является отношением частичного порядка на множестве подколец поля К. Максимальные элементы этого множества и только они являются кольцами Н. поля К. Если А- кольцо Н., а  - кольцо с тем же полем частных, что и А, то В также кольцо Н. и Вявляется локализацией кольца Апо нек-рому простому идеалу.
- кольцо с тем же полем частных, что и А, то В также кольцо Н. и Вявляется локализацией кольца Апо нек-рому простому идеалу.
 (тождественное отображение К).
(тождественное отображение К). - поле формальных степенных рядов над k. Сопоставление ряду
- поле формальных степенных рядов над k. Сопоставление ряду  его порядка п(а нулевому ряду
его порядка п(а нулевому ряду  ) продолжается до Н. с группой значений
) продолжается до Н. с группой значений  (аддитивная группа целых чисел) и кольцом Н.
(аддитивная группа целых чисел) и кольцом Н.  . Ассоциированная точка сопоставляет ряду
. Ассоциированная точка сопоставляет ряду  свободный член
свободный член  .
. наз. дискретным; о их кольцах Н. см. Дискретного нормирования кольцо. Описание всех Н. поля рациональных чисел см. в [4].
наз. дискретным; о их кольцах Н. см. Дискретного нормирования кольцо. Описание всех Н. поля рациональных чисел см. в [4]. и
и  следует, что
следует, что  . Пусть А- кольцо Н. vполя Кс группой значений
. Пусть А- кольцо Н. vполя Кс группой значений  - подполугруппа положительных элементов Г и М- мажорное множество в
- подполугруппа положительных элементов Г и М- мажорное множество в  . Отображение
. Отображение 
 является биективным (взаимно однозначным) отображением множества мажорных подмножеств из
является биективным (взаимно однозначным) отображением множества мажорных подмножеств из  на множество идеалов кольца А. При этом главным идеалам соответствуют мажоры, обладающие минимальным элементом. Простым идеалам тоже соответствуют мажоры специального вида, а именно: мажоры вида
на множество идеалов кольца А. При этом главным идеалам соответствуют мажоры, обладающие минимальным элементом. Простым идеалам тоже соответствуют мажоры специального вида, а именно: мажоры вида  где
где  - положительная часть нек-рой выпуклой подгруппы Нгруппы Г. Таким образом, устанавливается взаимно однозначное соответствие между простыми идеалами А и выпуклыми подгруппами группы значений Г.
- положительная часть нек-рой выпуклой подгруппы Нгруппы Г. Таким образом, устанавливается взаимно однозначное соответствие между простыми идеалами А и выпуклыми подгруппами группы значений Г. будет Н. поля Кс кольцом Н.
будет Н. поля Кс кольцом Н. 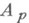 и идеалом Н. рА р ;кроме того, на поле
и идеалом Н. рА р ;кроме того, на поле  индуцируется Н. со значениями в группе Ни кольцом Н.
индуцируется Н. со значениями в группе Ни кольцом Н.  . Тем самым Н. расщепляется на более простые. Пусть А- кольцо Н., тогда простой спектр Абез нуля (Spec А-(0)) является линейно упорядоченным множеством и его тип наз. высотой, или рангом, соответствующего Н. Если Spec Аконечен, то высота Н. есть число элементов в Spec А-(0), и это число совпадает с числом выпуклых подгрупп группы Г, отличных от самой Г. Н. конечного ранга сводятся к Н. ранга 1. Последние характеризуются тем, что их группа значений - архимедова группа, т. е. изоморфна нек-рой подгруппе аддитивной группы
. Тем самым Н. расщепляется на более простые. Пусть А- кольцо Н., тогда простой спектр Абез нуля (Spec А-(0)) является линейно упорядоченным множеством и его тип наз. высотой, или рангом, соответствующего Н. Если Spec Аконечен, то высота Н. есть число элементов в Spec А-(0), и это число совпадает с числом выпуклых подгрупп группы Г, отличных от самой Г. Н. конечного ранга сводятся к Н. ранга 1. Последние характеризуются тем, что их группа значений - архимедова группа, т. е. изоморфна нек-рой подгруппе аддитивной группы  действительных чисел. В этом случае отображение
действительных чисел. В этом случае отображение  является ультраметрическим абсолютным значением поля К,
является ультраметрическим абсолютным значением поля К, Н. поля Kи
Н. поля Kи 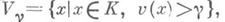 где
где  Совокупность всех
Совокупность всех  , образует фундаментальную систему окрестностей нуля топологии
, образует фундаментальную систему окрестностей нуля топологии  поля К, называемой топологией, определяемо й нормированием V. Топология
поля К, называемой топологией, определяемо й нормированием V. Топология  отделима и несвязна. Топология, индуцируемая
отделима и несвязна. Топология, индуцируемая  на кольце А, как правило, отлична от топологии локального кольца. Для нетривиального Н. поля Ктопология
на кольце А, как правило, отлична от топологии локального кольца. Для нетривиального Н. поля Ктопология  локально компактна тогда и только тогда, когда Н. vдискретно, кольцо Н. полное, а поле вычетов Н. vконечно; кольцо Апри этом будет компактно. Пополнение
локально компактна тогда и только тогда, когда Н. vдискретно, кольцо Н. полное, а поле вычетов Н. vконечно; кольцо Апри этом будет компактно. Пополнение  поля Котносительно топологии
поля Котносительно топологии  является полем; Н. vпродолжается по непрерывности до Н.
является полем; Н. vпродолжается по непрерывности до Н. и топология
и топология  совпадает с
совпадает с  . Кольцо
. Кольцо  нормирования vявляется пополнением кольца Анормирования v.
нормирования vявляется пополнением кольца Анормирования v. и
и  поля Кназ. независимым и, если топологии
поля Кназ. независимым и, если топологии  и
и  различны; это эквивалентно тому, что кольца нормирований
различны; это эквивалентно тому, что кольца нормирований  и .
и . порождают поле К. Неэквивалентные нормирования высоты 1 всегда независимы. Имеет место теорема аппроксимации для нормирований: пусть
порождают поле К. Неэквивалентные нормирования высоты 1 всегда независимы. Имеет место теорема аппроксимации для нормирований: пусть  - независимые нормирования,
- независимые нормирования,  тогда найдется такой элемент хполя К, что
тогда найдется такой элемент хполя К, что 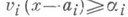 для всех
для всех  .
. - Н. поля L, а К- подполе L, то ограничение
- Н. поля L, а К- подполе L, то ограничение  нормирования
нормирования  на поле Кявляется Н. поля К, а его группа значений Г - подгруппой группы
на поле Кявляется Н. поля К, а его группа значений Г - подгруппой группы  наз. при этом продолжением Н. v. Обратно, если v- Н., a L расширение поля К, то всегда существует Н. поля L, продолжающее v. Индекс
наз. при этом продолжением Н. v. Обратно, если v- Н., a L расширение поля К, то всегда существует Н. поля L, продолжающее v. Индекс  подгруппы Г в группе
подгруппы Г в группе  наз. индексом ветвления Н.
наз. индексом ветвления Н.  относительно vи обозначается
относительно vи обозначается  Поле вычетов
Поле вычетов  нормирования vотождествляется с подполем поля вычетов
нормирования vотождествляется с подполем поля вычетов  степень расширения
степень расширения  обозначается
обозначается  и наз. степенью вычетов Н.
и наз. степенью вычетов Н.  относительно v. Продолжение
относительно v. Продолжение  нормирования vназ. непосредственным, если
нормирования vназ. непосредственным, если 
 - множество всех продолжений Н. v на L. Если L - конечное расширение поля Кстепени п, то множество всех продолжений vконечно, и
- множество всех продолжений Н. v на L. Если L - конечное расширение поля Кстепени п, то множество всех продолжений vконечно, и
 дискретно и либо Кполно, либо Lсепарабельно над К. Если L- нормальное расширение К, то продолжения
дискретно и либо Кполно, либо Lсепарабельно над К. Если L- нормальное расширение К, то продолжения  на Lпереводятся друг в друга K-автоморфизмами L, в частности если L- радикальное расширение К, то
на Lпереводятся друг в друга K-автоморфизмами L, в частности если L- радикальное расширение К, то  имеет единственное продолжение. В случае произвольного бесконечного расширения
имеет единственное продолжение. В случае произвольного бесконечного расширения  или продолжения
или продолжения  нормирования vстепень трансцендентности Lнад Кбольше или равна сумме
нормирования vстепень трансцендентности Lнад Кбольше или равна сумме  где
где  - степень трансцендентности расширения поля вычетов
- степень трансцендентности расширения поля вычетов  над полем вычетов
над полем вычетов  - размерность пространства
- размерность пространства 