|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
НОРМАЛЬНЫЙ ОПЕРАТОРЗначение НОРМАЛЬНЫЙ ОПЕРАТОР в математической энциклопедии: - замкнутый линейный оператор А, определенный на плотном в гильбертовом пространстве H линейном многообразии DA, такой, что Для Н. о. Аимеют место: 1) мультипликативное разложение
где U- унитарный оператор, однозначно определяемый на ортогональном дополнении подпространства нулей операторов 2) аддитивное разложение
где Из аддитивного разложения следует, что для упорядоченной пары Из этого разложения следует также, что Н. о. Аявляется функцией нек-рого самосопряженного оператора Важным свойством Н. о. является равенство Лит.:[1] Плеснер А. И., Спектральная теория линейных операторов, М., 1965; [2] Рудин У., Функциональный анализ, пер. с англ., М., 1975. В. И. Соболев. |
|
|
|

 , где
, где  - оператор, сопряженный с А. Если А- Н. о., то
- оператор, сопряженный с А. Если А- Н. о., то  Обратно, выполнение этих условий обеспечивает нормальность А. Если А-Н. о., то:
Обратно, выполнение этих условий обеспечивает нормальность А. Если А-Н. о., то:  также нормален;
также нормален;  - Н. о. при любых
- Н. о. при любых  нормален в случае, когда этот оператор существует, если
нормален в случае, когда этот оператор существует, если 
 где В- ограниченный линейный оператор, то также
где В- ограниченный линейный оператор, то также 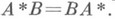

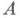 и
и  ;
;
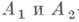 - однозначно определяемые самосопряженные операторы, перестановочные между собой.
- однозначно определяемые самосопряженные операторы, перестановочные между собой.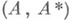 существует единственная двумерная спектральная функция
существует единственная двумерная спектральная функция 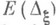 , где
, где 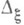 - двумерный интервал
- двумерный интервал 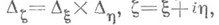 такая, что
такая, что 
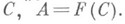 Обратно, всякая функция любого самосопряженного оператора есть Н. о.
Обратно, всякая функция любого самосопряженного оператора есть Н. о.
 из к-рого следует, что спектральный радиус Н. о. Асовпадает с его нормой
из к-рого следует, что спектральный радиус Н. о. Асовпадает с его нормой  . Собственные элементы Н. о., соответствующие различным собственным значениям, ортогональны.
. Собственные элементы Н. о., соответствующие различным собственным значениям, ортогональны.