|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
НОРМАЛЬНОЕ РАСШИРЕНИЕЗначение НОРМАЛЬНОЕ РАСШИРЕНИЕ в математической энциклопедии: поля - алгебраическое расширение Lполя К, удовлетворяющее одному из следующих эквивалентных условий: 1) любое вложение поля Lв алгебраич. замыкание 2) L- поле разложения нек-рого семейства многочленов с коэффициентами из K; 3) любой неприводимый над Kмногочлен f(x)с коэффициентами из K, имеющий корень в L, распадается в Lна линейные множители. Для любого алгебраич. расширения F/K существует максимальное промежуточное подноле L, нормальное над K, причем Для полей характеристики 0 любое нормальное расширение является расширением Галуа. В общем случае Н. р. является расширением Галуа тогда и только тогда, когда оно сепарабельно. Лит.:[1] Ван дер Варден Б. Л., Алгебра, пер. с нем., М., 1976; [2] Ленг С, Алгебра, пер. с англ., М., 1968; [3] Постников М. М., Теория Галуа, М., 1963. Л. В. Кузьмин. |
|
|
|

 поля Кявляется автоморфизмом поля L;
поля Кявляется автоморфизмом поля L; где
где  - всевозможные вложения поля Fв
- всевозможные вложения поля Fв  . Существует также однозначно определенное минимальное Н. р. поля K, содержащее F. Это поле является композитом всех полей
. Существует также однозначно определенное минимальное Н. р. поля K, содержащее F. Это поле является композитом всех полей  . Оно наз. нормальным замыканием поля Fотносительно K. Если
. Оно наз. нормальным замыканием поля Fотносительно K. Если 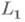 и
и  - нормальные расширения поля K, то пересечение
- нормальные расширения поля K, то пересечение  и композит
и композит 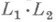 снова нормальны над K. Однако даже если расширения
снова нормальны над K. Однако даже если расширения 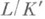 и
и  нормальны, расширение
нормальны, расширение  может и не быть нормальным.
может и не быть нормальным.