|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
НОРМАЛЬНО РАЗРЕШИМЫЙ ОПЕРАТОРЗначение НОРМАЛЬНО РАЗРЕШИМЫЙ ОПЕРАТОР в математической энциклопедии: - линейный оператор с замкнутой областью значений. Пусть А- линейный оператор с плотной в банаховом пространстве Xобластью определения и с областью значений R(А)в банаховом пространстве Y. Тогда А- Н. р. о., если чтобы область значений Аявлялась ортогональным дополнением к подпространству нулей оператора
(нормально разрешимое уравнение). Если Пусть ниже А- замкнутый оператор. Н. р. о. Аназ. п- нормальным, если его подпространство нулей N(А)конечномерно Н. р. о. Аназ. d-нормальным, если его дефектное подпространство конечномерно Пусть Xкомпактно вложено в банахово пространство
Оказывается, оператор А d -нормален тогда и только тогда, когда Следовательно, если
Пара чисел (п(А), d(A))наз. (d-характеристикой оператора А. Если Н. р. о. А n -нормален или d-нормален, то число
наз. индексом оператора А. Свойства n-нормальности и d-нормальности устойчивы: если А- п-нормален (d-нормален), а В - линейный оператор малой нормы или вполне непрерывный, то A+В n-нормален (d-нормален). Лит.:[1] Хаусдорф Ф., Теория множеств, пер. с нем., М.- Л., 1937, с. 266 - 90; [2] Аткинсон Ф., "Матем. сб.", 1951, т. 28, № 1, с. 3-14; [3] Крейн С. Г., Линейные дифференциальные уравнения в банаховом пространстве, М., 1971. В. А. Треногий. |
|
|
|

 т. е. если R(A)является замкнутым подпространством в Y. Пусть
т. е. если R(A)является замкнутым подпространством в Y. Пусть 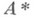 - оператор, сопряженный к А. Для того чтобы Абыл Н. р. о., необходимо и достаточно, чтобы
- оператор, сопряженный к А. Для того чтобы Абыл Н. р. о., необходимо и достаточно, чтобы  т. е.
т. е. Пусть дано уравнение с Н. р. о.
Пусть дано уравнение с Н. р. о.
 т. е. однородное сопряженное уравнение
т. е. однородное сопряженное уравнение  имеет только тривиальное решение, то R(A)=Y. Если же
имеет только тривиальное решение, то R(A)=Y. Если же  то для разрешимости (*) необходимо и достаточно, чтобы
то для разрешимости (*) необходимо и достаточно, чтобы  для всех решений уравнения
для всех решений уравнения 
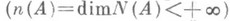

 . n-нормальные и d-нормальные операторы наз. иногда полуфредгольмовыми. Для того чтобы оператор Абыл n-нормальным, необходимо и достаточно, чтобы прообраз каждого компактного множества из R(А). был локально компактным.
. n-нормальные и d-нормальные операторы наз. иногда полуфредгольмовыми. Для того чтобы оператор Абыл n-нормальным, необходимо и достаточно, чтобы прообраз каждого компактного множества из R(А). был локально компактным. . Для га-нормальности Анеобходимо и достаточно наличие априорной оценки
. Для га-нормальности Анеобходимо и достаточно наличие априорной оценки
 n-нормален. При этом
n-нормален. При этом 
 компактно вложено в банахово пространство Z, то для d-нормальности Анеобходимо и достаточно наличие априорной оценки
компактно вложено в банахово пространство Z, то для d-нормальности Анеобходимо и достаточно наличие априорной оценки
