|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
НОРМАЛЬНАЯ КРИВИЗНАЗначение НОРМАЛЬНАЯ КРИВИЗНА в математической энциклопедии: регулярной поверхности - величина, характеризующая отклонение поверхности в направлении
где k- кривизна нормального сечения в направлении
Кривизна регулярной кривой, лежащей на поверхности, связана с Н. к. поверхности в направлении
(см. также Мёнъе теорема. С помощью Н. к. конструируется Дюпена индикатриса, гауссова и средняя кривизны поверхности и многие другие понятия локальной геометрии поверхности. Д. Д. Соколов. |
|
|
|

 от своей касательной плоскости в точке Р, совпадающая по абсолютной величине с кривизной соответствующего нормального сечения. Н. к. в направлении
от своей касательной плоскости в точке Р, совпадающая по абсолютной величине с кривизной соответствующего нормального сечения. Н. к. в направлении  равна
равна
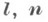 - единичный вектор главной нормали нормального сечения,
- единичный вектор главной нормали нормального сечения,  - единичный вектор нормали поверхности. Н. к. поверхности в данном направлении совпадает с Н. к. соприкасающегося параболоида в том же направлении. Н. к. поверхности, параметризованной параметрами и, v, может быть выражена через значения первой и второй квадратичных форм поверхности, вычисленных для значений
- единичный вектор нормали поверхности. Н. к. поверхности в данном направлении совпадает с Н. к. соприкасающегося параболоида в том же направлении. Н. к. поверхности, параметризованной параметрами и, v, может быть выражена через значения первой и второй квадратичных форм поверхности, вычисленных для значений  , соответствующих направлению
, соответствующих направлению  по формуле
по формуле
 , касательном к кривой, и с геодезич. кривизной
, касательном к кривой, и с геодезич. кривизной  этой кривой соотношением
этой кривой соотношением