|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
НИЛЬПОТЕНТНЫЙ ЭЛЕМЕНТЗначение НИЛЬПОТЕНТНЫЙ ЭЛЕМЕНТ в математической энциклопедии: нильпотент,- элемент акольца или полугруппы с нулем А, удовлетворяющий равенству
Если а- Н. э. индекса п, то справедливо равенство
т. е. элемент В коммутативном кольце Аэлемент анильпотентен тогда и только тогда, когда он содержится во всех простых идеалах кольца. Все Н. э. образуют идеал J, наз. нильрадикалом кольца и совпадающий с пересечением всех простых идеалов кольца А. Кольцо При интерпретации коммутативного кольца Акак кольца функций на пространстве Лит.:[1] Ленг С, Алгебра, пер. с англ., М., 1968; [2] Херстейн И., Некоммутативные кольца, пер. с англ., М., 1972; [3] Шафаревич И. Р., Основы алгебраической геометрии, М., 1972. Л. В. Кузьмин. |
|
|
|

 для нек-рого натурального п. Минимальное значение п, для к-рого справедливо это равенство, наз. индексом нильпотентности элемента а. Напр., в кольце вычетов по модулю
для нек-рого натурального п. Минимальное значение п, для к-рого справедливо это равенство, наз. индексом нильпотентности элемента а. Напр., в кольце вычетов по модулю  , где р- нек-рое простое число, класс вычетов числа р- нильпотент индекса п, матрица
, где р- нек-рое простое число, класс вычетов числа р- нильпотент индекса п, матрица является нильпотентом индекса 2 в кольце
является нильпотентом индекса 2 в кольце  -матриц с коэффициентами в нек-ром поле К, в групповой алгебре
-матриц с коэффициентами в нек-ром поле К, в групповой алгебре 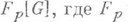 - поле из рэлементов, a G - циклич. группа порядка рс образующей а, элемент
- поле из рэлементов, a G - циклич. группа порядка рс образующей а, элемент  является нильпотентом индекса р.
является нильпотентом индекса р.
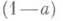 обратим в кольце Аи обратный к нему элемент записывается в виде многочлена от а.
обратим в кольце Аи обратный к нему элемент записывается в виде многочлена от а. уже не имеет Н. э., отличных от нуля.
уже не имеет Н. э., отличных от нуля.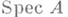 (спектре .4) нильпотентам соответствуют функции, тождественно равные нулю. Тем не менее рассмотрение нильпотентов часто оказывается полезным в алгебраич. геометрии, т. к. они позволяют получить чисто алгебраич. аналог ряда понятий, типичных для анализа и дифференциальной геометрии (бесконечно малые деформации и т. п.).
(спектре .4) нильпотентам соответствуют функции, тождественно равные нулю. Тем не менее рассмотрение нильпотентов часто оказывается полезным в алгебраич. геометрии, т. к. они позволяют получить чисто алгебраич. аналог ряда понятий, типичных для анализа и дифференциальной геометрии (бесконечно малые деформации и т. п.).