" 0 C F G H K L N P S T W Z А Б В Г Д Е Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш Э Ю Я

НИЛЬПОТЕНТНАЯ ПОЛУГРУППА

Значение НИЛЬПОТЕНТНАЯ ПОЛУГРУППА в математической энциклопедии:

- полугруппа Sс нулем, для к-рой существует такое п, что ; это эквивалентно выполнению в S тождества

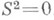Наименьшее для данной полугруппы число пс указанным свойством наз. ступенью (иногда классом) нильпотентности Н. п. Если , то Sназ. полугруппой с нулевым умножением. Следующие условия для полугруппы Sэквивалентны: 1) Sесть Н. п., 2) Sобладает конечным анну-ляторным рядом (т. е. возрастающим аннуляторным рядом конечной длины, см. Нильполугруппа),3) существует такое к, что любая подполугруппа из Sможет быть включена в идеальный ряд длины полугруппы S.

Более широким является понятие нильпотентной полугруппы в смысле Мальцева [2]. Так называется полугруппа, удовлетворяющая для нек-рого птождеству

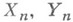где слова определяются по индукции следующим образом:

- переменные. Группа будет Н. п. в смысле Мальцева тогда и только тогда, когда она нильпотентна в обычном теоретико-групповом смысле (см. Нилъпотентная группа), причем выполнение тождества 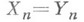эквивалентно тому, что ступень ее нильпотентности 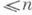. Всякая полугруппа с законом сокращения, удовлетворяющая тождеству вложима в группу, удовлетворяющую тому же тождеству.

Лит.:[1] Ляпин Е. С, Полугруппы, М., 1960; [2] Мальцев А. И., "Уч. зап. Ивановского гос. пед. ин-та", 1953, т. 4, с. 107 - 11; [3] Шеврин Л. Н., "Матем. сб.", 1961, т. 53, № 3, с. 367-86; [4] его же, там же, 1963, т. 61, № 2, с. 253-56.

Л. Я. Шеврин.