|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
НИЛЬПОТЕНТНАЯ ГРУППАЗначение НИЛЬПОТЕНТНАЯ ГРУППА в математической энциклопедии: - группа, обладающая нормальным рядом
таким, что каждый его фактор Конечные Н. г. исчерпываются прямыми произведениями р-групп, т. е. групп порядков Все Н. г. класса нильпотентности не больше с образуют многообразие (см. Групп многообразие), определяемое тождеством
Свободные группы этого многообразия наз. свободными нильпотентными группами. О пополнении Н. г. без кручения см. Локально нилъпотентная группа. Лит.:[1] Курош А. Г., Теория групп, 3 изд., М., 1967; [2] Каргаполов М. И., Мерзляков Ю. И., Основы теории групп, 2 изд., М., 1977. А. Л. Шмелькин. |
|
|
|
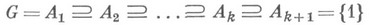
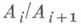лежит в центре факторгруппы 
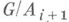(такой ряд наз. центральным). Длина наиболее короткого центрального ряда Н. г. наз. ее классом (или ступенью) нильпотентности. В любой Н. г. нижний (а также верхний) центральный ряд (см. Подгрупп ряд). обрывается на единичной подгруппе и имеет длину, равную классу нильпотентности группы.
, где р- простое число. В любой Н. г. элементы конечных порядков образуют подгруппу, факторгруппа по к-рой не имеет кручения. Конечно порожденные Н. г. без кручения исчерпываются группами целочисленных треугольных матриц с единицами на главной диагонали п их подгруппами. Любая конечно порожденная Н. г. без кручения аппроксимируется конечными р-группамп для любого простого р. Конечно порожденные Н. г. являются полициклическими, группами, более того, они имеют центральный ряд с циклич. факторами.