|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
НИЖНЯЯ ГРАНЬЗначение НИЖНЯЯ ГРАНЬ в математической энциклопедии: семейства топологий F(заданных на одном множестве X)- теоретико-множественное пересечение этого семейства топологий, т. е. Топология Свободная сумма пространств, получающихся при наделении множества Xвсеми отдельно взятыми топологиями из семейства F, канонически отображается на пространство Лит.:[1] Архангельский А. В., Пономарев В. И., Основы общей топологии в задачах и упражнениях, М., 1974. А. В. Архангельский. |
|
|
|
. Обозначается 
. Всегда 
- топология на X. Если топологии 
и 
заданы на множестве Xи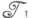 
содержится в 
(как множество), то пишут 
обладает свойством: если ,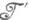 
- топология на Xи 
для всех 
, то 
. Важным свойством этого отображения является его факторность. На этой основе доказываются общие теоремы о сохранении ряда свойств при операции пересечения топологий.