|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
НЕЦЕНТРАЛЬНОЕ "ХИ-КВАДРАТ" РАСПРЕДЕЛЕНИЕЗначение НЕЦЕНТРАЛЬНОЕ "ХИ-КВАДРАТ" РАСПРЕДЕЛЕНИЕ в математической энциклопедии: нецентральное
где п - число степеней свободы, а
математич. ожидание и дисперсия равны соответственно Обычно Н. "х.-к." р. появляется как распределение суммы квадратов независимых случайных величин Если число пчетное, то функция распределения Н. "х.-к." р.
Эта формула устанавливает связь между Н. "х.-к." р. И Пуассона распределением. Именно, если Xи Yимеют распределения Пуассона с параметрами
Н. <<х.-к." р. часто возникает в задачах математич. статистики, посвященных исследованию мощности критериев типа "хи-квадрат". Так как существующие таблицы Н. "х.-к." р. недостаточно полны, то в статистич. приложениях широко используют различные приближения с помощью "хи-квадрат" распределения и нормального распределения. Лит.:[1] Большев Л. Н., Смирнов Н. В., Таблицы математической статистики, 2 изд., М., 1968; [2] Кендалл М., Стьюарт А., Статистические выводы и связи, пер. с англ., М., 1973; [3] Рatnaik Р. В., "Biometrika", 1949, V. 36, р. 202. А. В. Прохоров. |
|
|
|

 -распределение,- непрерывное, сосредоточенное на положительной полуоси
-распределение,- непрерывное, сосредоточенное на положительной полуоси  распределение вероятностей с плотностью
распределение вероятностей с плотностью
 - параметр нецентральности. При
- параметр нецентральности. При  =0 эта плотность совпадает с плотностью обычного (центрального) "хи-квадрат" распределения. Характеристич. функция Н. "х.-к." р. выражается формулой
=0 эта плотность совпадает с плотностью обычного (центрального) "хи-квадрат" распределения. Характеристич. функция Н. "х.-к." р. выражается формулой
 . Н. "х.-к." р. принадлежит классу безгранично делимых распределений.
. Н. "х.-к." р. принадлежит классу безгранично делимых распределений. имеющих нормальное распределение с отличными от нуля средними т i и единичными дисперсиями, точнее, сумма
имеющих нормальное распределение с отличными от нуля средними т i и единичными дисперсиями, точнее, сумма  имеет Н. "х.-к." р. с пстепенями свободы и параметром нецентральности
имеет Н. "х.-к." р. с пстепенями свободы и параметром нецентральности  Сумма нескольких взаимно независимых случайных величин с Н. "х.-к." р. имеет распределение этого же типа, и его параметры суть суммы соответствующих параметров слагаемых.
Сумма нескольких взаимно независимых случайных величин с Н. "х.-к." р. имеет распределение этого же типа, и его параметры суть суммы соответствующих параметров слагаемых. (всегда равная нулю при x<=0) при x>0 равна
(всегда равная нулю при x<=0) при x>0 равна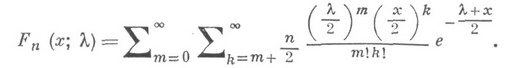
 и
и  соответственно, то для любого целого
соответственно, то для любого целого