|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
НЕФРЕДГОЛЬМОВО ИНТЕГРАЛЬНОЕ УРАВНЕНИЕЗначение НЕФРЕДГОЛЬМОВО ИНТЕГРАЛЬНОЕ УРАВНЕНИЕ в математической энциклопедии: - интегральное уравнение, для к-рого неверны те или иные Фредгольма теоремы. Иногда Н. и. у. наз. особым интегральным уравнением. Так, напр., интегральное уравнение Фурье
имеет решение
где а- произвольное положительное число; собственному значению
любое
Следовательно, для уравнения (2) перестает быть справедливой теорема Фредгольма о том, что множество собственных значений уравнения но более чем счетно. Подробно разработаны теории двух классов Н. и. у.: уравнений, в к-рых искомая функция содержится под знаком несобственного интеграла в смысле главного значения ( сингулярные интегральные уравнения);уравнения, в к-рых искомая функция содержится под знаком интегрального преобразования свертки ( интегральные уравнения типа свертки). Для таких уравнений, вообще говоря, нарушается равенство чисел линейно независимых решений однородных союзных (сопряженных) уравнений, а также альтернатива Фредгольма. Лит.:[1] Привалов И. И., Интегральные уравнения, 2 изд., М.- Л., 1937; [2] Петровский И. Г., Лекции по теории интегральных уравнений, 2 изд., М.- Л., 1951. См. также лит. при статьях Интегральное уравнение типа свертки и Сингулярные интегральные уравнения. Б. В. Хведелидзе. |
|
|
|



 уравнения (1) соответствует бесконечное множество линейно независимых решений, т. е. для уравнения (1) перестает быть справедливой теорема Фредгольма о том, что однородное уравнение имеет конечное число линейно независимых решений. В случае интегрального уравнения Лалеско - Пикара
уравнения (1) соответствует бесконечное множество линейно независимых решений, т. е. для уравнения (1) перестает быть справедливой теорема Фредгольма о том, что однородное уравнение имеет конечное число линейно независимых решений. В случае интегрального уравнения Лалеско - Пикара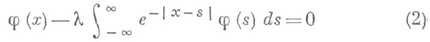
 является собственным значением, а именно, любому положительному числу
является собственным значением, а именно, любому положительному числу  соответствуют два линейно независимых решения:
соответствуют два линейно независимых решения: