|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
НЁТЕРОВО КОЛЬЦОЗначение НЁТЕРОВО КОЛЬЦО в математической энциклопедии: левое (правое)- кольцо А, удовлетворяющее одному из следующих эквивалентных условий: 1) А- левый (правый) нётеров модуль над собой; 2) любой левый (правый) идеал в Аимеет конечный базис; 3) любая строго возрастающая цепочка левых (правых) идеалов в Аобрывается на конечном номере. Примером Н. к. может служить любое кольцо главных идеалов, в к-рых любой идеал имеет одну образующую. Н. к. названы по имени Э. Нётер (Е. Noether), систематически исследовавшей такие кольца и перенесшей на них ряд результатов, известных ранее только при более жестких ограничениях (напр., теорию примарного разложения Л аскера). Кольцо нётерово справа не обязано быть нётеровым слева и наоборот. Напр., пусть А- кольцо матриц вида Факторкольцо и конечная прямая сумма Н. к. снова нётеровы, но подкольцо Н. к. может не быть нётеровым. Напр., кольцо многочленов над пек-рым полем от бесконечного числа переменных не является нётеровым, хотя оно содержится в своем поле частных, к-рое нётерово. Если А- нётерово слева кольцо, то кольцо многочленов А[х]также нётерово слева. Аналогичное свойство справедливо и для кольца формальных степенных рядов над Н. к. В частности, кольца многочленов вида Лит.:[1] Ван дер Варден Б. Л., Алгебра, пер. с нем., 2 изд., М., 1979; [2] Ленг С, Алгебра, пер. с англ., М., 1968; [3] Фейс К., Алгебра: кольца, модули и категории, пер. с англ., т. 1, М., 1977. Л. В. Кузьмин. |
|
|
|

 , где
, где 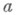 - целое рациональное число и
- целое рациональное число и 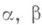 - рациональные числа с обычным сложением и умножением. Тогда Анётерово справа, но не нётерово слева, т. к. левый идеал элементов вида
- рациональные числа с обычным сложением и умножением. Тогда Анётерово справа, но не нётерово слева, т. к. левый идеал элементов вида  не имеет конечного базиса.
не имеет конечного базиса. или
или  где К- нек-рое поле, а
где К- нек-рое поле, а  - кольцо целых чисел, а также любые их факторкольца являются нётеровыми. Любое артиново кольцо нётерово. Локализация коммутативного Н. к. Аотносительно нек-рой мультипликативной системы Sснова является Н. к. В коммутативном Н. к. Адля любого идеала не такого, что все элементы вида l+m, где
- кольцо целых чисел, а также любые их факторкольца являются нётеровыми. Любое артиново кольцо нётерово. Локализация коммутативного Н. к. Аотносительно нек-рой мультипликативной системы Sснова является Н. к. В коммутативном Н. к. Адля любого идеала не такого, что все элементы вида l+m, где  , не являются делителями нуля, выполняется соотношение
, не являются делителями нуля, выполняется соотношение 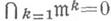 . Это соотношение означает, что любой такой идеал m определяет на Аотделимую nt-адическую топологию. В коммутативном Н. к. любой идеал представим в виде несократимого пересечения конечного числа примарных идеалов. Хотя такое представление не однозначно, но однозначно определены число идеалов в представлении и множество простых идеалов, ассоциированных с данными примерными идеалами.
. Это соотношение означает, что любой такой идеал m определяет на Аотделимую nt-адическую топологию. В коммутативном Н. к. любой идеал представим в виде несократимого пересечения конечного числа примарных идеалов. Хотя такое представление не однозначно, но однозначно определены число идеалов в представлении и множество простых идеалов, ассоциированных с данными примерными идеалами.