|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
НЁТЕРА - ЭНРИКЕСА ТЕОРЕМАЗначение НЁТЕРА - ЭНРИКЕСА ТЕОРЕМА в математической энциклопедии: о канонических кривых - теорема о проективной нормальности канонической кривой и об определяемости ее квадратичными уравнениями. Пусть 1) Xпроективно нормальна в 2) если 3) идеал IX порождается компонентами степени 2 во всех случаях, кроме следующих: а) X- тригональная кривая, т. е. обладает линейным рядом (системой) 4) в исключительных случаях а) и б) квадрики, проходящие через X, высекают поверхность F, являющуюся соответственно: а) неособой рациональной линейчатой поверхностью степени Эта теорема (в несколько иной, алгебраич. формулировке) была установлена М. Нётером [1]. Геометрич. изложение было дано Ф. Энрикесом (F. Enriques, о его результатах см. [2]; современное изложение в [3], [4], обобщение в [5]). Лит.:[1] Nother M., "Math. Ann.", 1880, Bd 17, S. 263-84; [2] Вabbage D. W., "J. London Math. Soc", 1939, v. 14, № 4, p. 310 - 14; [3] Saint - Dоnat В., "Math. Ann.", 1973, Bd 206, S. 157-75; [4] Шокуров В. В., "Матем. сб.", 1971, т. 86, № 3, с. 367-408; [5] Аrbarellо Е.., Sernesi E., "Invent, math.", 1978, v. 49, p. 99- 119. В. А. Псковских. |
|
|
|

 - гладкая канонич. кривая (негиперэллиптическая) рода
- гладкая канонич. кривая (негиперэллиптическая) рода  над алгебраически замкнутым полем ки
над алгебраически замкнутым полем ки  - однородный идеал в кольце k[ х п, ..., xg-1], определяющий Xв Р g-1. Теорема Нётера - Энрикеса (наз. иногда также теоремой Нётера - Энрикеса - Петри) утверждает, что:
- однородный идеал в кольце k[ х п, ..., xg-1], определяющий Xв Р g-1. Теорема Нётера - Энрикеса (наз. иногда также теоремой Нётера - Энрикеса - Петри) утверждает, что: ;
; , то X- плоская кривая степени 4, а если
, то X- плоская кривая степени 4, а если  , то градуированный идеал
, то градуированный идеал  порождается компонентами степени 2 и 3 (и это означает, что кривая Xявляется пересечением квадрик и кубик в
порождается компонентами степени 2 и 3 (и это означает, что кривая Xявляется пересечением квадрик и кубик в  через нее проходящих);
через нее проходящих); размерности 1 и степени 3, б) X- кривая рода 6, изоморфная плоской кривой степени 5;
размерности 1 и степени 3, б) X- кривая рода 6, изоморфная плоской кривой степени 5; причем ряд
причем ряд 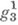 на Xвысекается линейной системой прямых на F, а при g=4 - квадрикой в
на Xвысекается линейной системой прямых на F, а при g=4 - квадрикой в  (возможно конусом), б) поверхностью Веронезе
(возможно конусом), б) поверхностью Веронезе 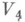 в
в  .
.